


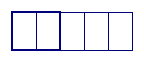
2. If the rectangle has a value of 2/5. show 1




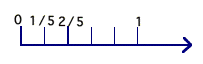



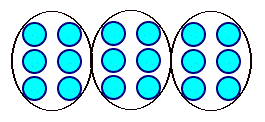





If this discrete collection has a value of 2/5, show 1
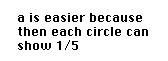
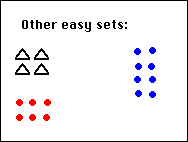
Tell 3 other discrete collections for which it would be easy to answer the problem:
If this discrete collection has a value of 2/5, show 1
We can also take an amount or a shape, and ask, if this is a part, what size is the whole? This is another good type of question for building understanding of fractions as part of a whole
You can print out these problems to work, and then look at my answers (move your cursor over the solution graphics)
The final question is:
What do the sets have in common for which it is easy to solve the problem:
" If this discrete collection has a value of 2/5, show 1"
What they have in common is that they have an even number of elements.
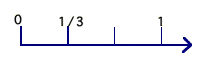
Notice that for each of these problems, I showed the associated unit fraction*, so if the problem said: this thing represents 3/4, I would find what 1/4 looks like; if the problem said: this thing represents 2/5, I would first show what 1/5 looks like. After that, I would use the right number of pieces that size to make a whole. The important thing, is that my shape or set be easily divisible by the number in the numerator, because that tells how many unit fractions there are in it.
If you didn't notice the unit fractions in my pictures, go back and look at them again. If you didn't show unit fractions on your work, go back and put them in--they're important for communicating the idea of size of a fraction.
*remember that a unit fraction is a fraction whose numerator is 1: it shows the size of a fourth, third, eighth, etc.