Solutions:
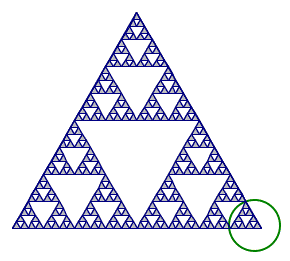
5A. For the circled similar part of this Sierpinski triangle, tell the scale factor needed to enlarge it to the whole triangle, and the number of copies needed to create the whole triangle.

The scale factor is 8, and the number of copies is 27:
The total length is as long as 8 widths of this sized triangles, so the enlargement scale factor is 8. |
There are 3 this size in the red circle (1, 2, 3). There are 3 red sized in a purple/pink, so that makes 9 so far (3+3+3). Then there are 3 of those to make a whole: 3x9=27 (9+9+9). |
B. Compare the number of copies for this scale factor to the copies needed for a 1D and 2D shape. What does this tell about the fractal dimension of the Sierpinski triangle?
A 1D shape with scale factor 8 would only need 8 copies (less than 27), and a 2D shape with scale factor 8 would need 8x8=64 copies (more than 27) so the Sierpinski triangle has a dimension between 1 and 2.
C. The dimension is log(27)/log(8) = 1.58 (rounded to 2 decimal places)
4A. For the smaller, similar part circled in this fractal, tell the scale factor to enlarge it to the larger whole curve, and the number of copies needed to create the larger whole curve.


The enlargement scale factor is 4
B. Compare the number of copies for this scale factor to the copies needed for a 1D and 2D shape. What does this tell about the fractal dimension of this fractal?
A 1D shape with scale factor 4 would only need 4 copies (less than 9), and a 2D shape with scale factor 4 would need 4x4=16 copies (more than 9) so the fractal has a dimension between 1 and 2.
C. The dimension is log(9)/log(4) = 1.58 (wow! that's the same as the answer for #5. It's pretty unusual for it to happen that you get exactly the same dimension for two fractals).
(more about fractal dimension here)