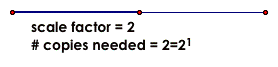
Fractal dimension:

Remember that if you have a self-similar 1-D shape, and you need a scale factor of F to get the big shape from the smaller one, then the number, N, of copies you need of the small size to make one of the large size is N=F=F^1

If you have a self-similar 2-D shape, and you need a scale factor of F to get the big shape from the smaller one, then the number, N, of copies you need is N=F^2

If you have a self-similar 3-D shape, and you need a scale factor of F to get the big shape from the smaller one, then the number, N, of copies you need is N=F^3

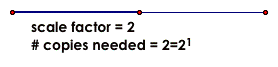
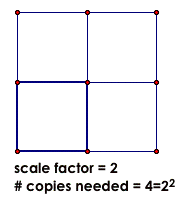
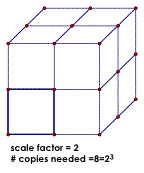
If the scale factor numbers aren't making sense to you, you may want to review scale factors

In general the self-similarity dimension (which is only one of many ways to define dimension) is the exponent d in the equation:

N=F^d

So, for the examples from the previous page, for the Koch curve we get one of these:

For the Sierpinski triangle, we got
F=8 and N=27
27=8^d
d=ln(27)/ln(8)=ln(3^3)/ln(2^3)=(ln3)/(ln2)= approx 1.58