Fractal dimension solutions: (printable)

1. I have a mystery shape that is self similar. I have a specific smaller similar copy of my mystery shape where the enlargement scale factor (the scale factor to make the larger copy from the smaller one) is 5.

A. If the mystery shape was 1-D, how many copies of the smaller shape would you need to build the larger shape?

5¹=5

B. If the mystery shape was 2-D, how many copies of the smaller shape would you need to build the larger shape?

5²=25

C. If the mystery shape was 3-D, how many copies of the smaller shape would you need to build the larger shape?

5³=125

2. I have a mystery shape that is self similar. I have a specific smaller similar copy of my mystery shape where the enlargement scale factor (the scale factor to make the larger copy from the smaller one) is 5. If I need 25 copies of the smaller shape to build the larger shape, what dimension is my shape?

2-dimensional because 5²=25

3. I have a mystery shape that is self similar. I have a specific smaller similar copy of my mystery shape where the enlargement scale factor (the scale factor to make the larger copy from the smaller one) is 5. If I need 15 copies of the smaller shape to build the larger shape, what dimension is my shape?

A dimension in between 1 and 2 because 15 is in between 5 and 25.
(You can get 1 point extra credit if you can use the formula on page 509 to write down exactly what the dimension is.)

4. In this Koch curve, circle two pieces that are the same shape as the whole curve, but at a different magnification. For each of your pieces, tell how much (length scale factor) you would need to magnify them to get the whole thing, and how many of them it takes to make the whole thing:

Many choices for solutions. Here are two:

	If I magnify this x3, I should get the whole thing (the enlargement scale factor to change small -> large is 3). It takes four pieces this size to make the whole
	If I rotate this, and magnify it x9 it will be the same as the whole thing (magnifying x3 would give me a piece the same size as in A); the enlargement scale factor is 9. It takes 16 pieces this size to get the whole thing

5A. For the circled similar part of this Sierpinski triangle, tell the scale factor needed to enlarge it to the whole triangle, and the number of copies needed to create the whole triangle.

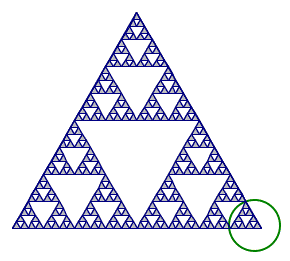
The scale factor is 8, and the number of copies is 27:

B. Compare the number of copies for this scale factor to the copies needed for a 1D and 2D shape. What does this tell about the fractal dimension of the Sierpinski triangle?

A 1D shape with scale factor 8 would only need 8 copies (less than 27), and a 2D shape with scale factor 8 would need 8x8=64 copies (more than 27) so the Sierpinski triangle has a dimension between 1 and 2.

6. In this fractal, circle a piece that is at the same shape as the whole thing, but at a different magnification. For your piece, tell how much (length scale factor) you would need to magnify it to get the whole thing (S), and how many of them it takes to make the whole thing (N). Then tell what dimension this fractal is, or what dimensions it is between.

If you circle pieces that are this size, then it take 5 of them to make the whole thing (n=5) and the scale factor is 3 (S=3)--the whole thing is 3 times as long.

With a scale factor of 3, a 1-dimensional shape would need 3 copies, and a 2-dimensional shape would need 9 copies. 5 is between 3 and 9, so this fractal's dimension is somewhere between 1 and 2.

7. In this fractal, circle a piece that is at the same shape as the whole thing, but at a different magnification. For your piece, tell how much (length scale factor) you would need to magnify it to get the whole thing (S), and how many of them it takes to make the whole thing (N). Then tell what dimension this fractal is, or what dimensions it is between.

If you circle pieces that are this size, then it take 5 of them to make the whole thing (n=5) and the scale factor is 5 (S=5)--the whole thing is 5 times as long.

With a scale factor of 5, if it were a 1-dimensional shape, it should take 5 of them to make the whole thing--and it does! So even though this doesn't look like a 1-dimensional shape, if you measure dimension this way--it is! That kind of makes sense because it looks a bit like it's a triangle--that would be 2-dimensional, and it looks a bit like just scattered individual points--that would be 0-dimensional, so this has dimension between 0 and 2--it has dimension 1.

8. In this fractal, circle a piece that is at the same shape as the whole thing, but at a different magnification. For your piece, tell how much (length scale factor) you would need to magnify it to get the whole thing (S), and how many of them it takes to make the whole thing (N). Then tell what dimension this fractal is, or what dimensions it is between.

The hardest thing about this fractal is finding the smaller pieces, because if you want the biggest ones, all of them are rotated from the directing in the big one. Here's how it works for the biggest pieces you could find:

S=2, N=3. With S=2, if it were 1-dimensional N would be 2 (it's not--it's bigger); if it were 2-dimensional, N would be 4 (it's not, it's smaller). Because N is between 2 and 4, the dimension is between 1 and 2.

Here's how it works with pieces 1-size smaller:

S=4, N=9. With S=4, if it were 1-dimensional N would be 4 (it's not--it's bigger); if it were 2-dimensional, N would be 16 (it's not, it's smaller). Because N is between 4 and 16, the dimension is between 1 and 2.

(more about fractal dimension here: not required for the Math 126 quiz, geeks only)

-