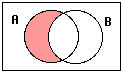Set notation

There is special notation that is used to describe interactions of sets. This notation is made of combinations of four symbols:

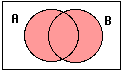
This is a union symbol. You write it between two sets names in the same way you write a + or – between two numbers. It means take all of both sets. If my sets are A: people who like apples, and B: people who like bananas, all of these mean the same thing:

People who like apples or bananas.

(notice that "or" goes between the two attributes or conditions that define the set)

Union means putting together. The United States is the union of the 50 states

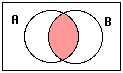
This is an intersection symbol. You write it between two sets names in the same way you write a + or – between two numbers. It means to take the overlap of the two sets. If my sets are A: people who like apples, and B: people who like bananas, all of these mean the same thing:

People who like apples and bananas

Intersection means an overlap or a meeting. When you drive through an intersection, the intersection is the overlap of the two streets.

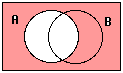
This is a complement symbol. You write it over the top of the name of a set. It means to take everything that is not in that set. If my sets are A: people who like apples, (and B: people who like bananas,) all of these mean the same thing:

People who don’t like apples

Complement means something like opposite: red and green are complementary colors. They are different, and between them they use the 3 primary colors (red, yellow, blue). (Note the spelling difference between complement and compliment)

Both of these symbols can represent set subtraction. We will use – in this class. You write it between two sets names in the same way you write a + or – between two numbers. It means to take everything that is in the first set, but not in the second set. You don’t ever have to use set subtraction, because you can do the same thing by combining intersections and complements, but it makes some things a lot simpler. If my sets are A: people who like apples, (and B: people who like bananas,) all of these mean the same thing:

A-B

People who like apples but not bananas.

Set subtraction is a lot like number subtraction in that it is a take-away concept, but it looks funny because the second set is not always a subset of the first set. You can’t just look at the number of elements in the sets in order to do a set subtraction, you actually have to look at the elements in the sets