There are two basic kinds of symmetry: line or reflection symmetry, where the shape looks the same on both sides of a mirror line, and rotational symmetry, where you can turn the shape through some angle and it will look the same as before you turned it. Children ususally learn about and can recognize reflection symmetry (gr K-2) before they can visualize rotational symmetry (gr 3-5)
| Line symmetry | Rotational symmetry |
 |
 |
Line symmetry is usually named by the line where you would put a mirror, showing how the two sides of the shape are reflections of each other. Depending on how you draw them or what font you use, some capital letters have symmetry lines. A letter A will (usually) have a vertical line going through its center where the A is the same on the left and right. Because the mirror line is vertical, we say A has vertical line symmetry. The letter D usually has a mirror line going horizontally through its center, and the D looks the same on the top and the bottom, so we say it has horizontal line symmetry. The letter H is interesting because it has two mirror lines--the vertical line through its center and the horizontal line through its center are both mirror lines, so H has both horizontal and vertical line symmetry. On the other hand G doesn't have any lines of symmetry--you can't split it into two halves that are exactly the same on both sides of a line.
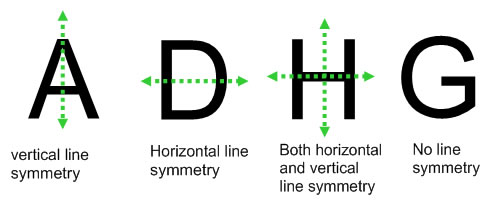
What examples can you think of? What other capital letters can you think of that have vertical line symmetry? What capital letters have horizontal line symmetry? What capital letters have both horizontal and vertical line symmetry? What capital letters have no line symmetry?
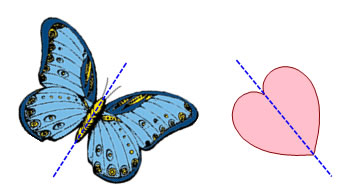
Symmetry lines don't have to be vertical, either. So long as the shape is the same (reflected image) on both sides of the line, it can be a symmetry line. This butterfly and heart have line symmetry across the lines I have drawn in, but we can't call it either horizontal or vertical lines symmetry, it's just line symmetry. If you want to, you can call it diagonal line symmetry.
There are more good examples of line symmetry at http://www.mathsisfun.com/geometry/symmetry-reflection.html
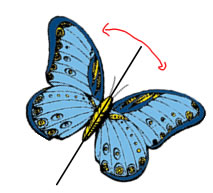
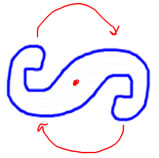
Rotational symmetry is when you have a shape that if you turn it you get the same thing. This is a concept that's best show with movement, so go push the play buttons under the order 2 and order 3 examples on this page: http://www.mathsisfun.com/geometry/symmetry-rotational.html
There are 3 ways to name rotational symmetry.
| Order: The order of the rotation is the number of times you turn around (symmetrically) before you get back to where you started. On the left, you turn the shape twice before you get all the way back, so it has rotational symmetry of order 2. On thr right, you can turn the shape 3 times before you get all the way back, so it has rotational symmetry of order 3. | 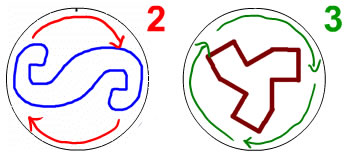 |
| Fraction of a turn: If you look at how far you turn the shape to get it to look the same, you can think of that as a fraction of how far you go to get all the way around. This fits in with fraction circles, so this vocabulary is often used in elementary school. On the left, you turn 1/2 way around, so it has half-turn symmetry. On the right, it turns 1/3 of the way around to look like itself again, so it has 1/3 turn symmetry. | 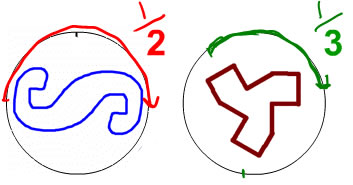 |
| Angle: When children start measuring angles with protractors, and describing angles in degrees (often 5th grade), then they also start describing turns in terms of number of degress. So, the 1/2 turn becomes 1/2 of 360° = 180°, and the 1/3 turn becomes 1/3 of 360° = 120°. Then we say the shape on the left has 180° rotational symmetry, and the shape on the right has 120° rotational symmetry. | 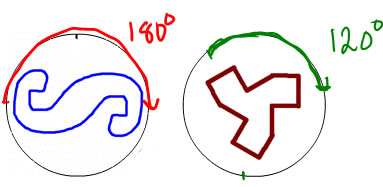 |
The most common kind of rotational symmetry is half-turn symmetry. Some of the capital letters have half-turn symmetry:

Each of these letters (N, S and H) look the same if you rotate them upside down. You can see this for yourself by writing the letters on a piece of paper, and then turning it upside down (so the top of the paper is on the bottom, and the bottom on the top). H has 3 kinds of symmetry: horizontal line symmetry, vertical line symmetry and half-turn symmetry. It turns out that if a shape has two kinds of line symmetry (like horizontal and vertical), then it will also have rotational symmetry, just like H does. N and S have rotational symmetry, but they don't have any line symmetry.
An interesting letter is O because it looks almost, but not quite like a circle.
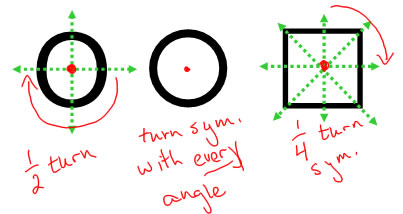
An O (and an X) are both just a little taller than they are wide, so a letter O is an oval and not a circle. If you turn an O by 90°, you'll find that it doesn't look quite like an O anymore. You have to turn the O a complete half turn to look just like itself again, so the letter O has half-turn symmetry. A circle, on the other hand, is so symmetric that it's hard to describe all of the symmetries. If you turn a circle through any angle around its center, it will be the exact same circle, so a circle has rotational symmetry through every angle (wow).
A square is more symmetric than the letter O, but less symmetric than the circle. If you turn a square 90°, it will look exactly like it was to start with, but if you turn it by an angle less than 90°, it won't look the same. A square has 1/4-turn rotational symmetry (or 90° rotational symmetry). It also has 1/2 turn symmetry, and it would be OK to say it has 1/4 turn and 1/2 turn symmetry, but we don't have to because 1/2=2/4: any shape that has 1/4 turn symmetry also has 2/4 and 3/4 turn symmetry, and 2/4 = 1/2, so when we say a shape has 1/4 turn symmetry that automatically means that it also has 1/2 turn symmetry.
I've also shown the reflection lines on the O and the square. The O has both horizontal and vertical line symmetry (2 symmetry lines), but because it's an oval and not a circle, if you put in a diagonal line, it won't quite work as a symmetry line. The square has 4 symmetry lines: horizontal, vertical and the two diagonal lines that go through the corners. If you take a square and fold it in half along the diagonal line that goes through the corners, you'll find that the triangular halves match up, so those are symmetry lines. (If I started drawing in symmetry lines in the circle, I wouldn't know where to stop, because any line I drew through the center of the circle would work.)
What other capital letters have rotational symmetry?
Some shapes (like the square we already looked at) have more lines of symmetry than just 2 and/or have rotational symmetry about an angle that's not just a half-turn. For now, we'll just look at this snowflake as an example:
| Just the snowflake | The snowflake and its symmetries |
 |
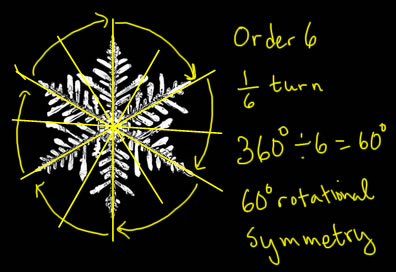 |
Where to start: The easiest symmetry line to see is the vertical one--it goes between the top and bottom "fingers" of the snowflake. That should help you see that there's a symmetry line going down each opposite pair of "fingers" (that's 3 symmetry lines).
The next place to look is half-way between the symmetry lines you have so far--between the "fingers"--is that a symmetry line? Yes! So that gives us the other 3 symmetry lines. (You could try the trick again, looking between adjacent symmetry lines, but that doesn't give you equal sides.
Real life isn't perfect: I know, I know, some of the little fingers of the snowflake go over some of those last 3 symmetry lines--how can that be? Anything you find in nature--a butterfly, a snowflake, your face, ... is going to be not quite perfect. There's some randomness as well as order to how a snowflake puts itself together, so all of these cool examples from nature are going to be only approximately symmetric (like the capital B where the top and bottom are not quite perfectly the same size). There are times when studying the symmetry (even though it's only approximate) in nature is a useful thing to do, and there are times when studying how things in nature are different from perfectg symmetry is a useful thing to do. Today we're looking for the symmetry.
Rotations? Let's look at the fingers again. All of the fingers of the snowflake look (approximately) alike--so a turn that kept it looking the same would rotate one finger to the next. If you look at all of those turns, there are 6 of them in a full turn, so the snowflake has 1/6-turn symmetry (it also has 2/6=1/3 turn symmetry, and 3/6 = 1/2 turn symmetry, but we only have to tell the 1/6 of the turn because everything else is made out of sixths).