Practice problems:

For each of these vertex-edge graphs, figure out whether it can be traced or not.  If it can be traced, tell a way to trace it.  If it can't be traced, tell how you know that it can't be traced



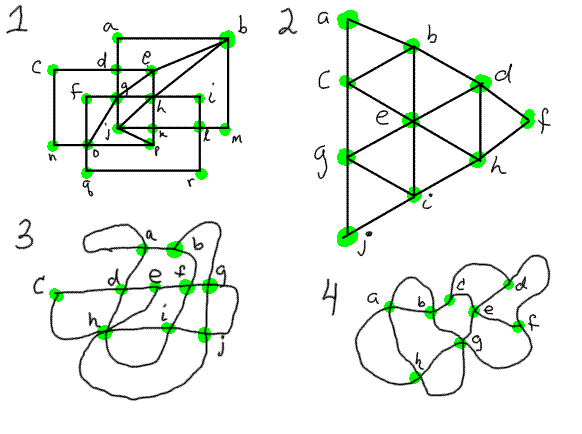
For each of these vertex-edge graphs, color in a big dot for each of the vertices, and name each vertex with a letter.   Then, figure out whether it can be traced or not.  If it can be traced, tell a way to trace it.  If it can't be traced, tell how you know that it can't be traced.



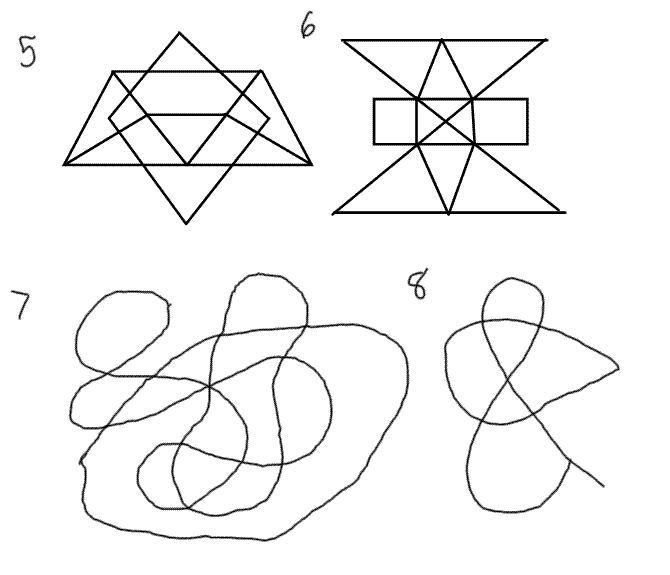
For each of these vertex-edge graphs, add in the smallest number of edges you can to make it traceable.

Answers