For each of these vertex-edge graphs, figure out whether it can be
traced or not. If it can be traced, tell a way to trace it.
If it
can't be traced, tell how you know that it can't be traced
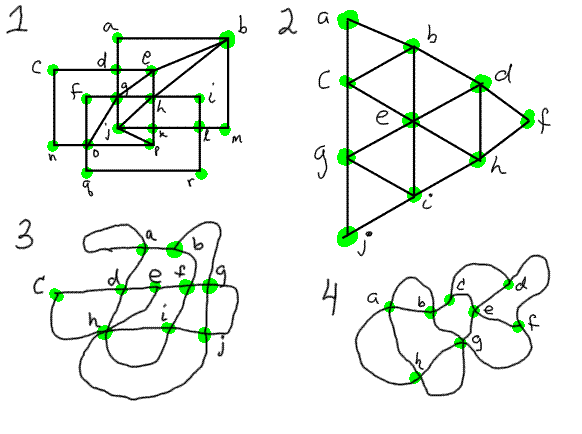
#1 can be traced. There are only 2 vertices of odd order: o and
p, so we must start and end at o and p. One way to trace is this
order:
o-p-k-h-e-d-c-n-o-f-g-h-i-l-r-q-o-g-d-a-b-m-l-k-j-g-e-b-h-j-p
#2 can be traced. All vertices have even order, so we sill start
and end at the same vertex. One way of tracing is this order:
a-b-d-f-h-d-e-b-c-e-g-i-e-h-i-j-g-c-a
#3 can be traced because there are only 2 vertices that have an odd
order: b, e, so we must begin and end at b and e (in some order).
One way to trace is:
b-g- (straight down)-j-h-e-f-g-(following the path to the right)-j-i-
(along upper path)-h-c-d-a-(go around loop)-a-b-f-i-(allong lower
path)-h-d-e
#4 can't be traced because there are more than 2 vertices that have an
odd order: c, d, and f each have 3 ways to get to them, and h has 5.
For each of these vertex-edge graphs, color in a big dot for each of
the vertices, and name each vertex with a letter. Then,
figure out
whether it can be traced or not. If it can be traced, tell
a way to trace it. If it can't be traced, tell how you know that
it
can't be traced.

#5: A few of these vertices: a, h, k, and s are optional and can be
omitted. This one can't be traced because it has more than
3 odd vertices: b, e, n and r all have 3 ways to get to them
#6: A few of these vertices: a, c, d, g, i, l, m and o are optional and
can be omitted. This one is traceable. All of its vertices
have even order, so you will start and end at the same place. One
way to trace is:
b-c-f-h-j-m-n-o-k-h-e-a-b-f-g-l-k-j-i-d-e-f-k-n-j-e-b
#7. All of these vertices are needed. All of these vertices are
even. This can be traced, and you will begin and end in the same
place. One tracing order is:
i-j-(path to left)-k-g-(straight up)-f-e-d-(top path)-i-b-a-(around
loop)-a-c-e-h-g-(left path)-f-h-k-(right path)-i-e-b-c-d-(straight
across)-i
#8: One of these vertices is optional (f). The vertex h is not
optional. Two of the vertices: h and g, have odd order so we must
begin and end at them. One way to trace is:
h-g-e-f-b-(straight across)-a-d-e-c-a-(top path)-b-c-d-g
For each of these vertex-edge graphs, add in the smallest number of
edges you can to make it traceable.

The vertices circled in red are all odd. We have to connect up
all but 2 of these to get a traceable graph. Below are some ways
of connecting those vertices with new edges so that the graph is now
traceable.

