Untitled Document

Area, Perimeter and Shape

Shapes can have the same area and have different perimeters.

Shapes can have the same perimeter and have different areas.

A big question in mathematics is to try and find the biggest or smallest of something. The area/perimeter questions about this are:

Of all of the shapes that have the same area, which shapes have the largest and smallest perimeters?
Of all of the shapes that have the same perimeter, which shapes have the largest and smallest areas?

Same perimeter: Here's an experiment with shapes that have the same perimeter:

I used a safety pin to pin together a ribbon

ribbon

I fit in as many cubes as I could in a line. The number of cubes in the ribbon show the area--area is the number of square units enclosed by the perimeter, and my cubes are square units.

cubes in a line

15 square units

Now I've moved the cubes so they don' thave to stay in a straight line (I haven't taken any out). There's room for lots more!

Wow--that's all the blank cubes I had in my bag, and it's still not full

more cubes

Luckily , dice are the same size. This is my biggest rectangle: it's an 8x8 square

8x8 square

64 square units!

If I take out the 4 corners from the rectangle, I can fit in a row of 5 more on the top and bottom: a net gain of 6.

more cubes

And I took out 4 more and put in 8 more on the sides--a gain of 4 cubes (it's starting to look more like an octagon or a circle)

still more cubes

74 square units

I tried to put in beans and pat them down gently to push against the sides, but the beans kept escaping. You can see, though, how the sides are bulging outwards in a kinda round way.

beans

Trying to cover even more area--not sure if I'm succeeding or not.

When the shape got rounder, it covered more area, when it was long and skinny it covered a small amount of area. When it was round and fat, it covered a larger amount of area..

Here are some more examples:

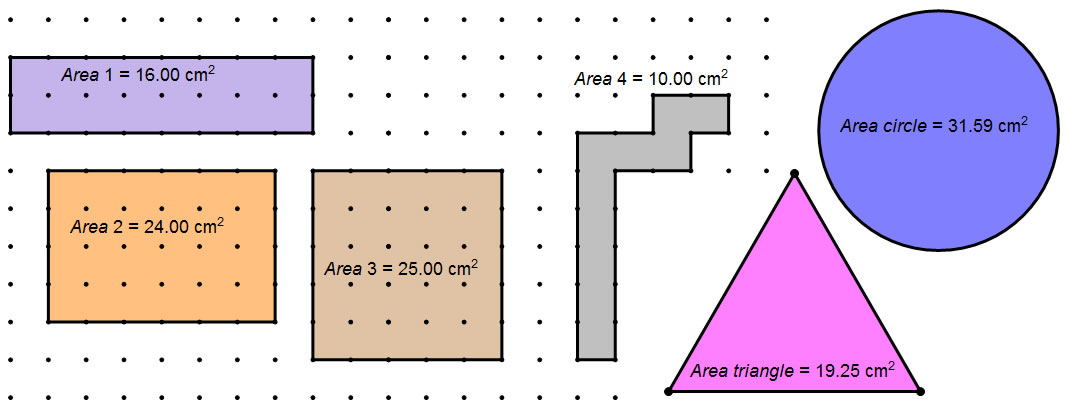
shapes with the same perimeter

All of these shapes have a perimeter of 20 cm. You can see that the one with the smallest area is only 1 cm wide, even though it snakes around. To make a small area, the shape should be narrow in one dimension. Out of the rectangles, the largest one is the square: when the side lengths are the same, the shape is as balanced as it can be and still be a rectangle. That gives it the biggest area. The only shape I have in this picture with a bigger area is the circle. The circle is the same width in every direction, which gives it the largest area.

Water is good at finding this special biggest area-smallest perimeter spot. If you slowly drop or pour water onto a flat surface, it will make a circular puddle. That's because the water is pushing out equally in all directions at once, while the surface tension tries to keep it's edge small and compact.

If you're experimenting just with rectangles, you'll find that the one with the biggest area is always as close to being a square as you can get with your materials--same dimensions in both directions.

Same area: Your homework task will be to do a similar experiment where the area stays the same.

Keeping the area the same is pretty easy. What you'll need is some square units. You can cut out unit squares from the grid paper page of the assignment and move them around physically, or you can count out square units as you draw onto grid paper.

In part a of the problem, you'll be making shapes with an area of 12 square units, and in part b you'll be making shapes with an area of 16 square units.
To find the pattern, you'll need to make several shapes that have 12 square units, and several shapes that have 16 square units, and find the perimeter of each shape. I want you to at least find all of the whole-number side rectangles that have 12 and 16 square units--other shapes are cool, but optional.

Example (with 8 square units): I can make a 1x8 rectangle, and a 2x4 rectangle with an area of 8 square units. The 1x8 rectangle has a perimeter of 18 units. The 2x4 rectangle has a perimeter of 12 units. The narrower rectangle has a longer perimeter.
You should compare all of the shapes with 12 square units to each other, and all of the shapes with 16 square units to each other.
Finally, you'll be writing up what the pattern appears to be: what kind of shapes (with the same area) have the longest perimeter? what kinds of shapes have the shortest perimeter?