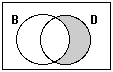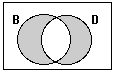2-Set Venn Diagrams

For every section of a Venn diagram, there might be elements that belong there. For example, if we look at how the sets: B = (mostly) Brown animals and D = Dogs relate in the universe of all Mammals, we can find examples of every possible combination of conditions

We describe can describe each small section in words by using the properties of the two sets:

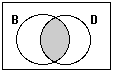
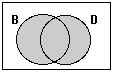
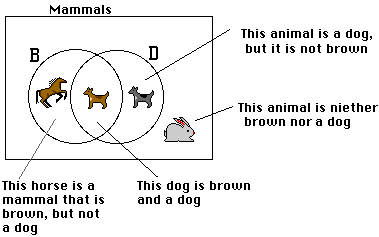
	This diagram shows the intersection: Mammals that are both brown and are dogs. ! Notice that I am saying that I want both conditions (brown and being a dog), which is more restrictive, not that I want both sets (all brown things and all dogs), which is more inclusive. This could be said more briefly: “this is the set of brown dogs”.
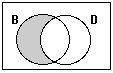
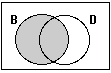
	This diagram shows the part that is in B that is not overlapping with D: Mammals that are brown and* are not dogs. or “Brown mammals that are not dogs”. ! It is important to have the “but not dogs” part of the sentence. If you say: “Mammals that are only brown’, that doesn’t give enough information, because you have to tell what it is that you are excluding *“and” could be replaced by “but”
	Mammals that are dogs but are not brown or “Dogs that are not brown” Notice that this sentence can be shortened dramatically because the primary set (D) is defined by a noun, whereas the previous example can’t be shortened as much, because the primary set (B) is described by an adjective
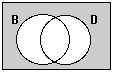
	Mammals that are neither brown nor are dogs. !Note the neither-nor construction. This is more specific than the not-or construction: “mammals that are not brown or dogs” which is ambiguous, and could mean either “mammals that are dogs or are not brown” or it could mean “mammals that are not either brown or dogs” (the second of these choices is the one that is the same as the neither-nor sentence .

Then there are shadings of the diagram that include more than one section. the most common ones are:

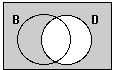
	Mammals that brown or are dogs. At first this picture may seem to include too much (what about the animals that are both?), but if you make it into a question that you are asking about the elements of the set, it makes more sense: If you have a picture of a brown animal or a dog, raise your hand. (the most natural thing, if you have a picture of a brown dog, is to raise your hand)
	Mammals that are brown or are dogs, but not both. ! If you don’t want the elements in the intersection, you have to exclude them.
	Brown mammals or “mammals that are brown” ! This one is tricky because it's too easy! Notice that the set D doesn’t affect the shading at all. You could erase it, and the picture wouldn’t change at all. compare this to the next picture. In that one, ...
	... you have to say something about D: Brown mammals that are not dogs, because the lines showing set D affect the shaded area, so the conditions on D affect the set

Think about it this way...

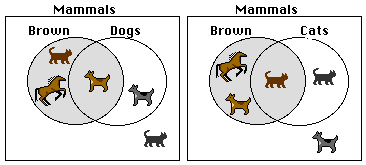
If I change the second set from Dogs to Cats, all of the same elements that were in the shaded area before are still in the shaded area. The definition of the second set didn’t affect what was included in the shaded area. The purpose of the defining phrases is to define and determine what properties shaded areas have, which is the same as determining what elements go in the shaded area.

Just like the previous shading wasn’t really affected by the set D conditions at all, this shading isn’t affected by the set B conditions at all, so this is the set of all mammals that are not dogs.

practice problems