Representations of Fractions

There are a lot of good representations of fractions that teachers and students should be familiar with. Different representations are useful for different types of problems.

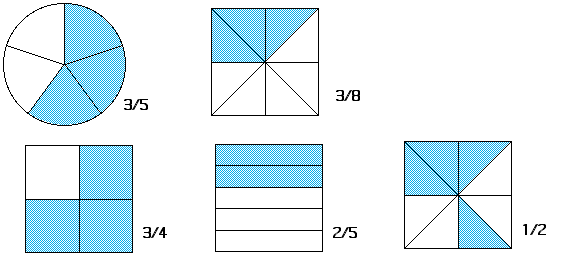
One of the most general is an area representation: this means that the fractional amount is shown by the amount of area covered by something. Fraction circles and fraction squares are both area models: the amount of area shows the fraction:

The key thing for an area diagram is that the area (usually the shaded area) shows the fraction. It is not necessary, for instance that the two halves in a diagram showing 1/2 be the same shape, only that they have the same area.

For circles, the areas are usually shown in only one way: as sectors. The most standard way for fractions of squares to be done is with dividing lines parallel to the sides (see the diagrams of 3/4 and 2/5 above), though a common exploration (about grade 3) is to investigate fractions of a square or rectangle, making many shapes that show the same fraction.

Another common model is a number line model. This can be shown either with a standard number line, or with fraction bars. Fraction bars are long skinny rectangles, but they are only ever divided on their length to show different fractions, never on their height:

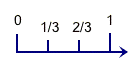
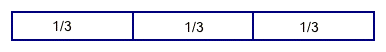
Finally, many fractions are fractions of a discrete set. A representation is discrete if you think of its members not being divisible, so a bag of Jolly Ranchers, or a group of people would be discrete (you can't easily break a Jolly Rancher in half, and you can't have half of a person), but a plate of brownies would not be discrete (you can share a brownie more easily than sharing a Jolly Rancher. I'm going to use small circles most of the time to show discrete sets, but you could draw candies, or balloons, or anything else that comes in ones, but not in halves:

If I have a set of 4 dots, I can use it to show fourths and halves, but not thirds.

Next