In the following problems, you may find it useful to use the triangle applet

3. Finish filling in the chart showing how triangle properties can overlap, and explain the properties that cannot overlap:

	Scalene	Isosceles	Equilateral
Right
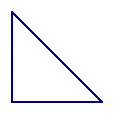Acute
Obtuse

Specifically:

• Draw a table like this, and for each of the places in the table where it is possible to do so, draw an example of a triangle that fits both conditions (eg. the example given is both isosceles and right). Make sure that your example triangles are big enough and well drawn enough to show the properties they are supposed to show.
• For a few of the places in the table it will not be possible to make a triangle that has both properties. For each of these spaces, write an explanation of why it is impossible to have a triangle with both properties (you may label and write these explanations below--you don't have to fit them into the small space in the table)

4. Draw a Venn diagram (with example triangles in every region that one could possibly be in) showing the relationship between right triangles, obtuse triangles and acute triangles

5. Draw a Venn diagram (with example triangles in every region that one could possibly be in) showing the relationship between acute triangles and isosceles triangles.