1. List important prerequisite ideas for learning to multiply with multiples of 10 and 100.
Understanding place values and the commutative law of multiplication. Also helpful is knowing 1-digit multiplication facts, and the array model of multiplication.
2. How does thinking in tens help with multiplying 4x60?
You can think of it as 4 x 6 tens of 4 groups of 6 tens, which is 24 tens=240. so if you know 4x6=24, you can use it to find 4x60 because 4x60 is 4x6 tens.
3. How do manipulatives help with learning to multiply with 2- and 3-digit numbers?
They help children see that the multiplication of the whole number is the sum of multiplying in each place value.
4. Why are proportional materials like base 10 blocks good manipulatives for learning multiplication?
Proportional materials are good because children can see visually the comparitive sizes of the numbers.
5. Why are non-proportional base 10 materials good for learning multiplication?
Non-proportional materials are good for doing problems with large numbers where you wouldn't have enough room to show all of the manipulatives for the whole problem if they were proportional in size.
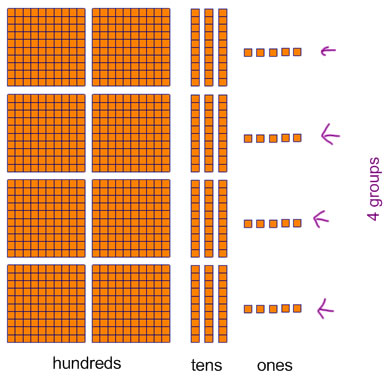
6. Take out your base 10 blocks and build the multiplication problem 235x4
I hope you set up your materials in some sort of an array, where you can see simultaneously the 4 groups of 235 and you can also see the hundreds together, and the tens together and the ones together. Here's what my picture looks like:

7. Sketch what it would look like to build the multiplication problem 462x4 using either the Montessori stamp game or the round manipulatives pictured in Primary Mathematics.
Again, arrays are almost always a good choice for multiplication, especially with multi-digit numbers. Here's my picture.

8. Write out an informal/child invented way of multiplying (with numbers, not manipulatives) 462x4
There are lots of possibilites. Here are two:

9. Compute 462x4 using
a. the expanded algorithm
b. the standard/traditional algorithm
c. the lattice algorithm
