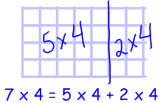This lecture covers a lot of ground:
A representation is a way of showing multiplication. A model for multiplication is slightly more sophistocated and it is comprised of several related representations that all have the same structure. There are two models for multiplication that we'll be comparing and using in this lesson: repeated addition and array/area.
Repeated Addition is a model for multiplication. All of the diagrams we used for the word problems in lesson 4.1 are repeated addition representations, beacause they are most clearly abstracted as a repeated addition of numbers:
Direct Modeling with equal sets generally shows a repeated addition of equal amounts. For example:
shows 6+6+6+6+6
Multiplication bar diagrams show repeated addition of equal amounts represented by equal sized bars:
shows 4+4+4
shows 5+5+5
And Numerical repeated addition such as 4×7=7+7+7+7 is a representation of a repeated addition interpretation of multiplication
Arrays (Rectangles and Area) is another common and important model for multiplication.
An array is a way of arranging the the repeated sets so that you can either count along rows or up and down along columns:
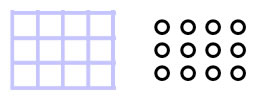
These diagrams each show 3 rows of 4 (3×4) and 4 columns of 3 (4×3).
This representation turns out to be really helpful for seeing patterns. It's also a useful representation in higher grades when we study area and start multiplying fractions.
An array model and representation for multipliacation helps us understand...
The commutative law (or commutative property) says that the order of the two numbers that you're multiplying doesn't matter. If you think about it, that's kind of surprising. It means that:
6+6+6+6+6 = 5+5+5+5+5+5
If youre just adding up a bunch of one number and a bunch of the other, there doesn't seem to be any reason why the answers would be the same, but they are. Drawing an array picture helps, because you can see that the same array can be counted as 5 rows of 6 = 6+6+6+6+6 = 5×6 or it can be counted as 6 columns of 5 = 5+5+5+5+5+5 = 6×5.
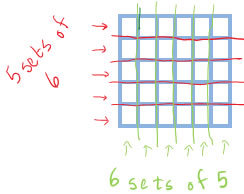
Arrays and the commutative property change our view of multiplication so fundamentally, that they even change the words we use to describe it. Before we realized that multiplication was commutative, we used the words multiplicand and multiplier to describe the numbers we were multiplying:
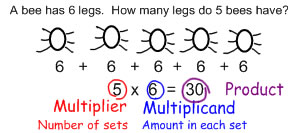
multiplier × multiplicand = product
The multiplier is the number of sets, and the multiplicand is the amount in each set so if the multiplier is 4 and the multiplicand is 6 then the relationship is
4×6 = 6+6+6+6 = 24
and if the multiplier is 6 and the multiplicand is 4, then the relationship is:
6×4 = 4+4+4+4+4+4=24
With the commutative property, however, we realize that it doesn't matter which is the multiplier and which is the multiplicand, and so we call both of those numbers factors:
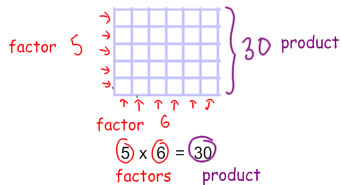
factor × factor = product
The commutative law is helpful because it lets you choose from two ways to compute. So, for 5×6, you can choose to find the product by adding 5 sixes or by adding 6 fives.
When children are learning multiplication facts, this means that there are fewer facts to memorize, since by learning 5×6, you also have learned 6×5.
Explaining the commutative law (with all the details)
Here is an example of a commutative law explanation:
 |
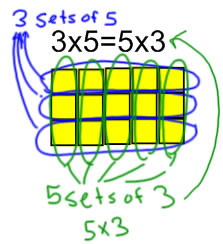I can group the array into horizontal rows, and when I do I get 3 rows of 5 squares (which is 3×5 squares). I can also group the array into vertical rows and when I do I get 5 rows of 3 squares (which is 5×3 squares). Counting 3 rows of 5 and counting 5 rows of 3 are two ways of finding the amount of squares in this same array. |
In this explanation, I have ringed the groups and used arrows to show how to see the set as both 3 sets of 5 and 5 sets of 3.
I also used arrows and labels to show that 3 sets of 5 = 3×5 and 5 sets of 3 is 5×3.
I wrote a sentence explaining that the way the diagrams show the properties is by being two ways of counting the exact same amount.
The distributive property (or distributive law) provides a way of breaking down products into smaller chunks.
For instance, you could figure out 7×4 by first multiplying 7×5 and 7×2 and then adding those together. You can show this with an array:
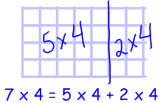
You can also reason it out by using repeated sets thinking. If 7×4, think of 7 as the multiplier (the number of sets). So if I have 5 sets of 4 and 2 sets of 4 that makes 7 sets of 4 in all. 5×4+2×4=7×4
The distributive property can also be used in a subtractive way:
10 sevens is one more 7 than 9 sevens, so if you know how much 10 sevens is, you can take away 1 seven to get the right amount for 9 × 7
9 × 7 = 10 × 7 - 1 × 7
Arrays are really helpful if you want to think of splitting the multiplicand instead of the multiplier. For instance, when doing 6×12, we want to break 6 twelves into 6 tens and 6 twos. An array format is helpful to see that these are the same:
Explaining the distributive law
Here are 3 ways of explaining the distributive law. They each have a picture and sentences that match and explain the picture. They each come from a different way of thinking about multiplication. Practice explaining the distributive law in the way that makes the most sense to you.
Explanation 1 (arrays)
|
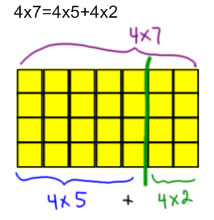
The 4 by 7 array is made of two smaller arrays, so I can find the total number of squares 4×7 by finding the squares in the smaller parts: 4×5 and 5×2 and adding them together |
Explanation 2 ( 4 sets of 7)
|
7 is equal to 5 and 2 more so 4 sets of 7 is the same as 4 sets of 5 and 2 more I can find out how many in all by finding how many are in 4 sets of 5 (4×5) and how many are in 4 sets of 2 (4×2) and adding them together. |
Explanation 3 (7 sets of 4--uses the commutative law to switch the order)
|
4×7=7×4 is seven sets of 4 That's 5 sets of 4 and 2 more sets of 4 So I can find the amount in 5 sets of 4 (5×4) and the amount in 2 sets of 4 (2×4) and add them together to find the amount in 7 sets of 4. |
According to the Common Core standards, children should be learning the times table in third grade. Teach will, however, need practice in fourth and fifth grade to cement their multiplication knowledge. In third grade it's most important for children to learn efficient strategies for figuring out multiplication facts, and drill for speed should follow work with efficient ways of computing.
The easiest facts to learn are those for 0, 1 and 10. 0 and 1 are obvious once you know what it means to multiply by 0 or 1. 10 is easy because you can think of 10 as the multiplicand: 4×10 means 4 tens which is 40.
Next children learn facts for 2× and 5×. The best strategies for these, though, are quite different.
To multiply by 2, it's most efficient to think of 2 as the multiplier, so 2×8 = 8+8. If children know their doubles addition facts, they already have the 2× facts memorized.
To multiply by 5, however, it's most efficient (for most people) to think of 5 as the multiplicand. Doing 8 fives by counting by 5 is faster than doing 5 eights. Multiplying by 5 also has lots of cool patterns to discover (what happens when you multiply 5 by an even number?)
The rest of the facts are built on the 2× and 5× facts, so...
To multiply by 3: double the number and add it on again. For example 3×8 = 2×8 + 8 (double 8 and add 8)
To multiply by 4: double twice. For example: 4×8 = 2×8+2×8 = 2×(2×8) (double 8 to get 16, and then double 16 to get 32)
To multiply by 6: multiply by 5, and then add the number on again. For example 6×8 = 5×8 + 8
To multiply by 9: multiply by 10, and then subtract the number off. For example: 9×8 = 10×8 - 8
Using the commutative law, these strategies cover everything in the times table up to tens except for 4 (really 3) facts:
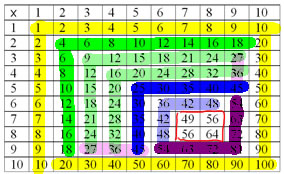
So, 7×7, 7×8 and 8×8 are left to be rote memorized. You'll probably find some kids that have strategies for figuring those out from ones they already know, too, but for a lot of kids, those ones are best learned through songs, rhymes, dumb jokes. Things like that.
More about 5's and 7's
5-times tables have some cool patterns that help with memorization. The easiest one to find is the pattern with multiplying by an even number:
5 × 2 = 10
5 × 4 = 20
5 × 6 = 30
5 × 8 = 40
The tens digit is half of the number being multiplied by 5. The math behind the pattern has to do with 5: 5 is half of 10 so...
5 × 2 = 10
5 × 4 = 5 × (2 × 2) = (5 × 2) × 2 = 20
5 × 6 = 5 × (2 × 3) = (5 × 2) × 3 = 30
5 × 8 = 5 × (2 × 4) = (5 × 2) × 4 = 40
7-times problems can be broken down using 5's in the same way 6's can be, using 7 = 5 + 2 and the distributive law. For example:
7 × 6 = (5 + 2) × 6 = 5 × 6 + 2 × 6 = 30 + 12 = 42
Think: 7 sets of 6 is 5 sets of 6 and 2 more sets of 6.
More about 9's:
9-times patterns come from knowing that 9 is one less than 10.
Look for the pattern:
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 × 5 = 45
9 × 6 = 54
9 × 7 = 63
9 × 8 = 72
9 × 9 = 81
You should notice that the tens digit is one less than the number you multiply by 10. You might also notice that the tens and the ones digits add up to 9. You can use that to figure out all of the 9's multiplication facts.
For example: 9 × 7 will have a tens digit one less than 7 (6) and the two digits will add up to 9 (6+_=9 so _=3). That gets you 63.
Now, this works because 9=10-1
9 × 7 = (10 - 1) × 7 = 10 × 7 - 1 × 7 = 70 - 7 = 63
If I subtract a 1-digit number from 70, I'm going to get 6_ (sixty-something). If I subtract 10-7=3, I'm going to get 3+7=10. 6 is one less than 10 so 3+6=9.
