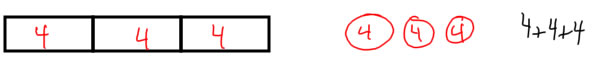Multiplication and Division Lesson 1: Multiplication models, properties and basic facts

Practice questions

1. Draw several diagrams and/or interpretations for 3×4 (your work will be judged on the completeness of the variety of models represented).

You should have a picture that shows a direct modeling-type diagram--something where 3 sets of 4 objects are shown, and you could count all of the objects to get the answer.  Something like this:

You should also have a picture that shows a repeated addition picture, where 3 sets are shown and the number of objects is represented using a number.  Any of these would be OK. For a perfect score, you should include both the first one (bar diagram) and the last one (repeated addition with numbers):

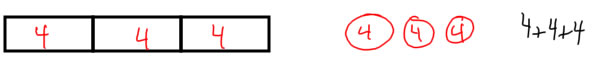
You should have a rectangle or an array diagram. For example:

There are always more variations you could include, but these are the main ones  I would be looking for. You could grade your work on this problem out of 10 points, giving 3 points each for one of the main types, and 1 more point if you included both a bar diagram and a repeated addition with numbers.

2. Explain these words mean:

• multiplier: the number of repeated sets in a multiplication problem.
• multiplicand: The amount in each set in a multiplication problem
• factor: either of the numbers (number or sets or amount in each set) multiplied together in a multiplication problem
• product: the result (total) of multiplying numbers.

3. Draw a diagram and write an explanation of the commutative property using 4×6=6×4 as an example.

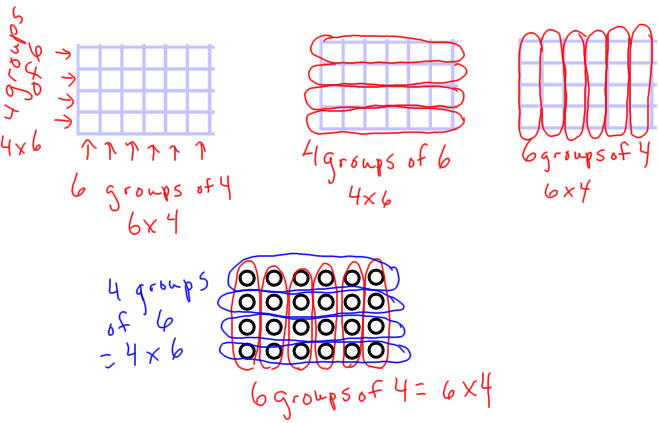
• You should be showing either a rectangle diagram (with subdivisions) or an array diagram with sides 4 and 6. 
• The diagram should be labelled either by drawing arrows or lines to indicate groups, or by circling to indicate gropus.
• These also need to be labelled as "4 groups of 6 = 4×6" and "6 groups of 4 = 6×4". 
• This is ideally done on a single diagram, but can also be done with two identical diagrams side-by-side.  If you use a pair of diagrams rather than a single diagram, it's preferred to have them both in the same orientation (for example 4 down and 6 across on both). Here are several examples:

You must also have at least one sentence describing the relationship. If you have labelled your diagram well, it can be pretty short.  Something like:

This shows that the same set can be viewed either as 4 sets of 6 or as 6 sets of 4, so those amounts have to be the same and 4×6=6×4.

I'd be really impressed if you said something about the general case, like:

No matter what numbers we use to make the rectangle (or array), it will always look like two different things if you look across or if you look down, so the turn around facts (where you switch the numbers in the multiplication) are always equal.

If your diagram isn't labelled, you'll have to do a lot more writing, so you're describing how to see the 4 groups of 6 by looking at the rows and how to describe the 6 groups of 4 by looking down the columns. 

4. Draw a diagram and write an explanation of the distributive property using 3×8 = 3×5+3×3 as an example.

You should have an array or rectangle diagram of some sort, split to show the two parts: 3×5 and 3×3, with labels for 3×8. 3×5 and 3×3 (ideally all on the same diagram).

You also need an explanation of one of these types:

• This diagram shows 3×8 (3 rows of 8), and we can see that the same diagram can be split into two parts: 3 rows of 5 on the left = 3×5 and 3 rows of 3 = 3×3 on the right. When you put them together, you get 3×8, so you can find the number of squares in 3×8 by adding 3×5 + 3×3.
• To find how many in 8 groups of 3, we can first find how many in 5 groups of 3, and then add on the number in 3 groups of 3, because 5 groups and 3 groups makes 8 groups (of 3).

5. Describe several ways to figure out the product: 4×7 (assume that "you" don't have 4×7 (or 7×4) memorized, though "you" do know some other multiplication facts).  Tell which of the strategies you described was the most efficient, and what made it efficient (efficient means that you were able to find the answer quickly using that strategy).

The most obvious ones would be repeated addition both ways (or skip counting both ways):

4+4+4+4+4+4+4 (4, 8, 12, 16, 10, 24, 28) and 7+7+7+7 (7, 14, 21, 28)

You should definitely be including the suggested one from the lecture:

double and double again: 2×7=14 and 2×14=28

You should recognize that doubling twice is more efficient than skip counting.

You might also come up with some more efficient strategies if you assum that you know some other multiplication facts:

If you know 4×6=24, then you can add one more 4 to get 28 (more efficient)

If you know 4×5, you can add 2 more 4's to get 24, 28 (more efficient)

If you know 5×7, you can subtract 7 to get 28. (probably less efficient--subtraction is harder for most students)

If I were writing a rubric for the "show several ways to do" part of this problem, I would give full points to something that included repeated addition/skip counting, doubling twice, and at least one other method.  I would give 4/5 for something that included both versions of skip counting/repeated addition and doubling twice. 

6. Describe how to solve 6×9 using the distributive property by using:

a. the strategy for 6

6×9 = 5×9 + 9 = 45 + 9 = 54

b. the strategy for 9

6×9 = 6×10 - 6 = 60 - 6 = 54

7. Describe strategies for figuring out:

• 2× Double the other number
• 3× Double the other number, and add the number on one more time
• 4× Double the other number and then double the result again
• 5× Count by 5's
• 6× Multiply the other number by 5 and then add the number on one more time
• 9× Multiply the other number by 10 and then subtract the number.