Multiplication and Division Lesson 2: Multiplying 2- and 3-digit numbers by 1-digit numbers

This lecture is fairly short (concise), and includes information on the following topics:

• The order for teaching multiplication of multidigit numbers by 1 digit numbers
• Materials for teaching multiplication of multidigit numbers by 1 digit numbers
• The expanded and standard algorithms for multiplication of multidigit numbers by 1 digit numbers

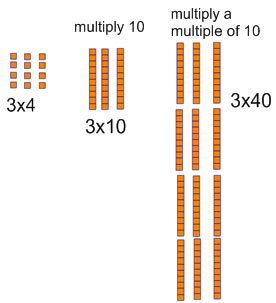
The first step in teaching and learning how to multiply multidigit numbers, is learning how to multiply a 1-digit number by a multiple of 10, 100 or 1000. The first step is to realize that 3x10 is 3 tens, so the product is 30, and 3x100 is 3 hundreds, so the product is 300. Next we compare 3x4, and 3x40 (and 3x400). If we build 3x40 with base 10 blocks, we get the same 3-across 4-down array as we make for 3x4, but now the array is made of tens, so 3x40 is (3x4) tens or 12 tens = 120.  This creates a nice pattern with the numbers too.  3x4=12 and 3x40 = 120: the 0 in the tens place in 40 corresponds to the 0 in the tens place in 120.  This pattern continues with hundreds too.  3x400 = 1200. This pattern makes multiplying by a multiple of 10 or 100 easy if you know your 1-digit multiplication facts. Children should practice with these problems before moving onto problems with 2- and 3-digit numbers.
The next step is to put two place values together. We can show 3x14 with base 10 blocks. It's easy to see with the materials that 3x14 consists of 3x4 and 3x10, and the we can find the total by taking the two products and adding them together
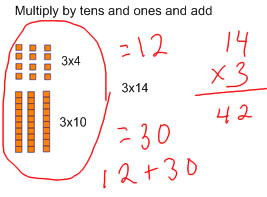
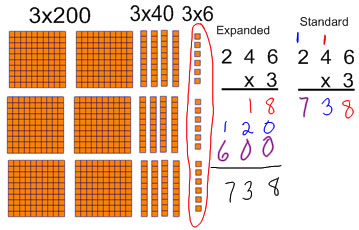
There are two main ways we can write down this process of getting the product. We can write down in an expanded form each of the products we get from each place value, and then add them together, or we can condense our work by adding place values as we go along (this is what the standard algorithm does).  If you are recording your work in the expanded algorithm, it's important to be careful with each of your products and give them the correct place value (12 tens, not 12 ones). 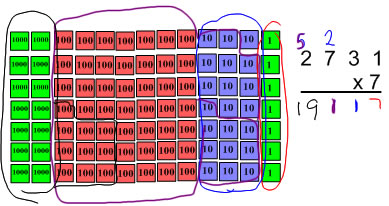When I am recording the standard algorithm, I try to explain the "carry" step as recording the 2 tens (from 4x6) above the 3 because 4 x 3tens will be a number of tens rather than explaining that I am writing it in the tens place.  This sounds a bit silly here when we are multiplying only by 1-digit numbers, but it contributes significantly with making sense with place value when you move to multiplying by 2-digit numbers where the place value of the product is not the same as the place value of the digit in the top row.
At some point before we move to multiplying 3-digit numbers, we have to practice computing a product where we are multiplying just by the 100's place.
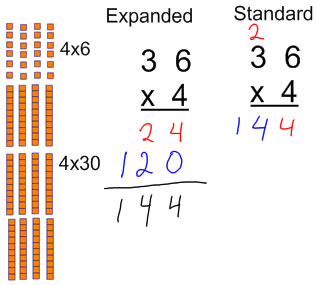
Then we compute some problems where we build the product with manipulatives, and we record. Eventually, we want children to learn and adopt efficient ways of writing down multiplication problems, but for some children it's helpful to spend time with the expanded algorithm before going to the standard algorithm because it shows more clearly the steps that we do to figure out a multi-digit product. After doing some problems with manipulatives, children should be encouraged to move to doing problems with pencil and paper alone as soon as they feel confident doing so.
Multi-digit multiplication is one place where having non-proportional materials is really useful, because you can extend the size of problems that can be solved using materials.  The physical size of base 10 blocks makes it difficult to solve problems that are very large, but you can easily extend your manipulative work into the thousands if you have a non proportional material (such as the Montessori stamp game) that you can use to represent hundreds and thousands.

At each stage along the way, children should be doing a significant amount of practice of pencil and paper work following learning with manipulatives.  Multiplication takes practice. If you can arrange your schedule to make it possible, it is better to do a smaller amount of practice (6-10 problems, depending on the length of the problems) distributed over several days than to do the same amount of practice at one time. This is particularly helpful for children who have a harder time learning math.

A review by the topics first listed:

• The order for teaching multiplication of multidigit numbers by 1 digit numbers
  • first teach multiplying by 10, 100, 100 and multiples of those, like 40, 400 and 4000
  • Show using base 10 manipulatives how multiplying a 2-digit (or 3-digit) number by a 1-digit number breaks down into the products in each digit, and then you add them together, 
  • Show how to record the product using the expanded algorithm (optional)
  • Show how to record the product using the standard algorithm
• Materials for teaching multiplication of multidigit numbers by 1 digit numbers
  • Base 10 blocks are good multi-purpose manipulatives, but they are physically too large to model large multiplication problems, so it's nice to have some non-proportional materials too (non-proportional means that the materials showing 100 are the same size as those showing 1 rather than being 100 times larger.
• The expanded and standard algorithms for multiplication of multidigit numbers by 1 digit numbers
  • In the expanded algorithm, you write out the product with each digit separately.  Make sure that you have the right place value for each product.
  • The standard algorithm is what you probably are in the habit of using.  In the standard algorithm, the notation is compressed, and adding in place values happens as you go along.
  • Some children benefit from learning the expanded algorithm first, because it shows more clearly what each of the partial products are
  • Most children benefit from distributed practice--fewer problems a day, but spread out and practiced consistently for at least a week.