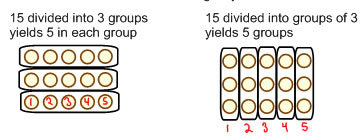
Usually the first experiences we give children with division are with numbers that can be evenly divided. There's are two really important principles that children should be exposed to with numbers that can be evenly divided.
15 ÷ 3 = 5 15 ÷ 5 = 3 3 × 5 = 15 5 × 3 = 15
The inverse of multiplication
Not all division problems give you a whole number answer. Division with remainders gives you the closest multiplication that is less than the dividend, and then you add on the remainder:
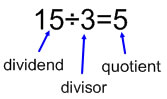
When we divide, the amount that is being divided up is called the dividend. In 15 ÷ 3 = 5; 15 is the dividend, 3 is the divisor and 5 is the quotient |
 |
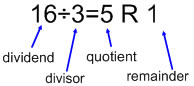
If there is the remainder, then the other parts of the equation keep the same names, but a remainder is also added on at the end. In 16 ÷ 3 = 5 R 1; 16 is the dividend, 3 is the divisor, 5 is the quotient, and 1 is the remainder |
 |
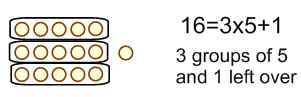
The division 15 ÷ 3 = 5 corresponds to the multiplication 3 × 5 = 15 The division 16 ÷ 3 = 5 R 1 corresponds to the same multiplication because when multiplying by 3, 3 × 5 is the closest you can get to 16 without going over 16. The equation that shows how the numbers are related by multiplication is: 3 × 5 + 1 = 16 the remainder is added to the product to yield the dividend. |
 |
Partitive division
When direct modeling division, you must choose to either show a partitive picture or a measurement picture. A partitive picture for 16 ÷ 3 would have 16 divided into 3 groups:
Measurement division
A measurement division picture would have 16 divided into groups of 3:

In different problems, the remainder has different affects on the answer. Consider these examples:
Ex. 1: Five children will share 14 cookies. How many cookies will each child get? How many will be left over?
Notice that this problem asks specifically for the remainder as well as the product. When we work out this problem, we find that each child gets 2 cookies, and 4 cookies are left over.

What happens to the remainder is that it is left over, as the question suggests. Each child gets 2 cookies--the quotient.
Ex. 2: There are 12 cookies. I will give 5 cookies to each child. How many children get cookies?
This problem questiond doesn't specifically ask for the number left over, but it's clear when we work out the problem that 2 children get 5 cookies each and that the other 4 cookies are left overs.

Again, in this context, the remainder is just an amount left over, and the answer to the main question is the quotient: 2 children get cookies.
Ex 3: There are 14 children. A van can hold 5 children. How many vans are needed to take all of the children?
My picture is the same for this problem as for example 2, but I have to do something different with the remainder this time

Because the remainder can't be discarded this time, we add one more to the quotient: 3 vans are needed to take all of the children, which is one more than the quotient.
Ex. 4: 5 children will share 14 cookies. How many cookies will each child get?
If you change the first example just a little--so that you're not assuming that the remainder is just an amount left over, theres another answer you can get.
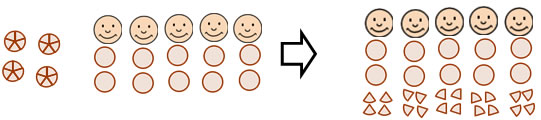
If we make the assumption that the cookies can be broken or cut into pieces, we can give the children partial cookies to use up the remainder, so that each child gets 2 4/5 cookies. The whole number 2 part of the answer is the whole number quotient. The fraction part of the answer has the remainder in the numerator and the divisor in the denominator.
![]()
This problem, FYI, is a little too hard for second or perhaps even third grade, but if we had 4 children sharing 15 cookies so that the cookies could be shared by making halves and quarters the problem would not be too hard for second grade. Children can solve problems with fractions in second grade if the fractions are friendly to think about, and the friendliest fractions are halves and quarters (beause a quarter is half of a half).
Ex 5: I made 14 cookies. If I make as many plates of 5 cookies each as I can for the bake sale, how many cookies will be left over for me?

This is kind of an unusual question, because it isn't asking for the groups at all--it's asking for the remainder.
The 3rd grade Common Core Math Standards include multiplying and dividing within 100. Division with higher numbers can also be modeled either with a partition or a measurement interpretation. Deciding which one is easier sometimes depends on the numbers.
Ex 6: 58 ÷ 9=?
In this example, if you make groups of 9, you won't have very many groups, but if you made 9 groups that would be kind of messy.

Direct modeling with base 10 blocks or linking cubes grouped in tens we get 6 groups with a remainder of 4
Let's show how this corresponds to multiplication for the same problem. Looking at it as a missing number multiplication, we want to know how close we can get to 58 by doing 9 × a number:
9 × 2 = 18 9 × 3 = 27 9 × 4 = 36 9 × 5 = 45 9 × 6 = 54 9 × 7 = 63 9 × 6 = 54 is as close as we can get to 58 without going over 58, so 58 ÷ 9 = 6 with some remainder. To find the remainder, subtract 58 - 54 = 4 so the complete answer is 58 ÷ 9 = 6 R 4 The long division process and notation is another way of representing what we just did with thinking about multiplication |
 |
Ex 7: 58 ÷ 4 =?
Here, we are dividing by 4, which would give us a relatively small number of groups if we think of it as partitioning, so that's the easiest way to model it.

So we have 14 in each group (the quotient) and a remainder of 2.
In this example, you see something really useful happening: we can put a whole ten in each group before exchanging. That also corresponds to how we long divide with numbers. This very convenient thing happens any time your dividend is a lot (more than 10 times) larger than the divisor. When children start dividing still larger numbers, this partition strategy is even more efficient.
Here's how to see that same thinking with long division:

And we can also do this with multiplication. I'm going to record my multiplication thinking in a way that's called the scaffolding algorithm for division. It's called "scaffolding" division because it supports learners as they get closer to being able to use long division.

This thinking is related to the thinking we do about 2-digit multiplication.
Because 4 × 10 = 40 and 4 × 4 = 16, we know that 4 × 14 = 40 + 16 = 56
Then we can say 4 × 14 + 2 = 58
The names of the parts of a division problem are dividend ÷ divisor = quotient R=remainder
Division problems can be figured out either by direct modeling using either a partition or a measurement division interpretation.
Division problems can also be figured out by thinking about the missing number multiplication problem.
If the dividend isn't divided evenly (if there's a remainder), then when multiplying you need to ask yourself: what can I multiply the divisor by to get as close as possible to the dividend without going over that number.
The multiplication way of representing this relationship is divisor × quotient + remainder = dividend
If the dividend is more than ten times as much as the divisor, then its helpful to use a partition interpretation when using manipulatives, because that lets you put tens into each group before exchanging.
You can make connections between the steps you do when direct modeling a division problem, and the steps you do when using long division.
When you have a division word problem that has a remainder, the sensible answer to the word problem question can be:
The right answer to the question depends on making sense of what the question is asking. Sometimes, either the "quotient" or the "quotient + a fraction" answer would make sense, and what you as a teacher might be looking for depends on what the class is studying.