There are essentially two ways of thinking of division:
Partition division (also known as partitive, sharing and grouping division) is a way of understanding division in which you divide an amount into a given number of groups. If you are thinking about division this way, then 12 ÷ 3 means 12 things divided evenly among 3 groups, and we wish to know how many is in 1 (each) group.
Measurement division (also called repeated subtraction division), is a way of understanding division in which you divide an amount into groups of a given size. If you are thinking about division this way, then 12 ÷ 3 means 12 things divided evenly into groups of 3, and we wish to know how many groups we can make.
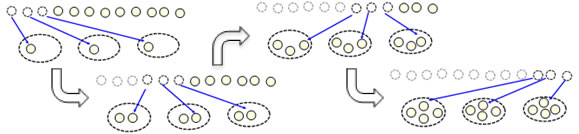
Direct modeling:These two ways of thinking of division correspond to two different ways to direct model to find the result of dividing.
Dividing 12 by 3 in a partitive way involves taking 12 objects and "dealing" them out evenly into three groups. Typically each counter is moved separately, and this takes 12 steps:

(On the Children's Mathematics Children's Strategies CD, you can watch a boy doing this. In the Multiplication & Division tab, watch Direct Modeling, Partitive Division--that version has the interesting detail that the boy uses a different colored Unifix cube to represent the sets)
Dividing 12 by 3 in a measurement way involves taking 12 objects and making groups of 3 from them. With a small number (3) in each group, this is typically a faster process because 3 counters are removed at a time, so this might take only 4 steps.
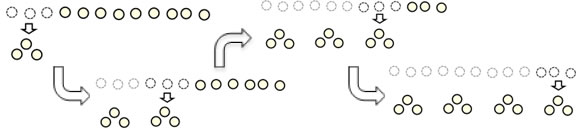
(On the Children's Mathematics Children's Strategies CD, you can watch a boy doing this. In the Multiplication & Division tab, watch Direct Modeling, Measurement Division)
While the answer you get in each case is the same, it represents different things. In the partitive interpretation, 4 is the number of objects in each group; in the measurement interpretation, 4 is the number of groups.
This makes division really tricky. One of the big things to learn about division is that both of these things are division, and they both give you the same numerical answers. This ties into multiplication being commutative. The commutative law of multiplication says that 3 groups of 4 is the same amount as 4 groups of 3. You know the answer to the partitive question 12 divided into 3 groups if you know that 3 groups of 4 is 12. You know the answer to the measurement question 12 divided into groups of 3 if you know that 4 groups of 3 is 12.
We can make the same array picture we did for multiplication to explain the two different versions of division:

Now, the two different direct modeling pictures we made for 12 ÷ 3 also show that 4 groups of 3 and 3 groups of 4 are the same amount (12), but when you are making your groups that way it seems really surprising that it should be true (Wow! You mean when you put 12 into 3 groups, there are 4 in each group, so 3 groups of 4, and when you put 12 into groups of 3, you get 4 groups, so that's 4 groups of 3? That's really cool how the numbers just switch around that way. I wonder if that works for any other numbers?). On the other hand, when you put them in an array, you can see that you just make the groups up and down for one grouping and side to side for the other grouping, so it's obvious that you should get the same number both ways (Well, duh, of course it's the same numbers when you switch it around--you're just counting in the opposite direction).
So--understanding the commutative law of multiplication, lets you start to understand that both ways of thinking of division will give you the same answers and you can use them interchangeably. That's really useful, because sometimes you can figure out the answer more quickly by one method than another. On the Children's Mathematics Children's Strategies CD, you can watch how quickly a girl solves a measurement division by skip counting (In the Multiplication & Division tab, watch Counting, Measurement Division). In the next interview (In the Multiplication & Division tab, watch Derived Facts, Partitive Division), the girl solves a partitive division problem with the same numbers. She remembers from the previous problem that 7 groups of 3 is 21, but she doesn't have a commutative law perspective on multiplication yet, she doesn't make the connection that 3 groups of 7 is also 21, and so she goes through some pretty complicated mental arithmetic steps to convert those 7 groups of 3 into 3 groups of 7 (very cool thinking, by the way--you can tell that she has a really good grasp on numbers).
Word problems are almost always either measurement division or partitive division problems. It's a useful thing for a teacher to be able to recognize which category different word problems fall into, and some of the ways children might go about solving the various problems. We'll look at the 4 types of problems that are discussed in the Children's Mathematics book.
Grouping problems are the most basic. Usually they are problems about discrete*, physical objects that are grouped in a fairly familiar.
*discrete means indivisible. These are things you count by 1's rather than measuring in feet and inches (and half-inches, etc).
In these grouping examples, the objects are cookies, and they are grouped by putting them on plates.
Partitive example:
I have 24 cookies. I want to put them on 4 plates, so that I have the same number of cookies on each plate. How many cookies should I put on each plate?
You can tell this is a partitive problem because it tells how many plates (groups of cookies) there are, and asks how much is on 1 (each) plate.
A child could direct model this by acting out putting equal numbers of cookies on 4 plates until they are all gone. A child who was figuring this out by counting, would probably guess and check to find the solution (if I have 2 on each plate, how many is that? What if I have 5 on each plate? etc.)
Measurement example:
I have 24 cookies. I want to put 4 cookies on each plate. How many plates do I need to hold my cookies?
You can tell this is a measurement problem because it tells how many go on 1 (each) plate, and asks how many plates (groups) there are.
A child could direct model to figure this out by making groups of 4 from a set of 24 counters. A child could figure this out by skip counting up by 4's until they reached 24, and keeping track of the groups as they counted up, or they could figure this out (probably on paper) by subtracting 4's from 24 until all were gone.
Price or cost problems are often appropriate for solving by direct modeling if the numbers are small enough. In price problems, the amount being grouped or shared is the money--the total cost, and it is grouped by the price per item. So, if it is a problem about buying pencils, then the total cost will be grouped by the cost for each pencil, and a single group is the price of a single pencil.
Partitive example:
4 pencils cost 36 cents. How much does one pencil cost?
The cost of 36 cents must be divided among the 4 pencils. (Cost per pencil is one group)
Measurement example:
A pencil costs 8 cents. How many pencils can I buy for 24 cents?
The total cost is again divided among several pencils, but this time the price for one pencil is known, and the number of pencils (groups) in unknown.
Rate problems are a more general version of the sort of thinking involved in price problems. Whereas price problems involve a price per item (cost for 1 item), general rate problems can relate a wider variety of things. Miles per hour is the most familar rate for most of us (relating distance--miles, and time--hours), but there are lots of others: words per minute (reading or typing), bushels per acre (corn or other crops), miles per gallon. Rate problems are usually appropriate for children at the age when they are familiar with the things being compared. In these examples, if children had experience (perhaps in science) with measuring distances things moved, and elapsed time with stop watches, these problems would be appropriate.
Partitive example:
It takes a battery powered toy train 5 seconds to go 20 inches. How far does the train go in 1 second?
The amount being divided up is the 20 inches travelled, and these are grouped into the distance travelled in each second. The group in problems like this is often indicated by the sentences: "how far ... in 1 second?"
Measurement example:
A toy train goes 6 inches in 1 second. How long will it take for the train to go 24 inches?
This uses the same type of total amout and way of grouping, but here we don't know how many groups (how many seconds).
Multiplicative comparison problems use or ask for a comparison by explicitly using multiplication in the description. For these ones, it's helpful to compare not just the two kinds of division, but also compare division to multiplication.
Multiplication example:
A farmer has 6 ducks. He has 3 times as many chickens as ducks. How many chickens does he have?
Partitive example:
A farmer has 3 times as many chickens as ducks. He has 18 chickens How many ducks does he have?
Measurement example:
A farmer has 6 ducks and 18 chickens. The farmer has how many times as many chickens as ducks?
The multiplication and partition division examples have very similar wording, because they both have the multiplicative comparison statment: "[the farmer] has 3 times as many chickens as ducks", which is a description of the relationship in size between two groups--the total, and the comparison group. The measurement example is worde quite differently, and indeed is kind of awkward.
A key to understanding multiplicative comparison problems that include a comparison (such as "[the farmer] has 3 times as many chickens as ducks"), is to realize that the comparison group takes the place of the unit groups in grouping problems. So, the number of ducks becomes a comparison group that lets you group chickens into groups that are as big as the duck group.
Thus, in a multiplication problem, you are told the amount in the comparison group, and you consider 3 groups of chickens, each of which has the same number as the amount of ducks--3x6.
In a (partition) division problem, you are told the total number (of chickens) and once you partition them into 3 equal groups you can find out what size one group of chickens is, and that is the same as the number of ducks. If you imagine doing this by direct modeling, you can see that you would be doing the same process when you split the chickens into 3 groups as you do in a grouping partition division problem.
Multiplication and partitive division problems of this type are also easy to represent with bar diagrams:

In the measurement division problem, what you are looking for is the multiplicative comparison. You need to know how many times the total number of chickens is when compared to the comparison group of ducks. If you imagine direct modeling this, you would be making groups of 6 chickens, and then you can see how many groups of 6 corresponds to the total of 18 chickens. Measurement division problems of this type don't really fit with the others, and make most sense when approached as a separate type of problem from the others.
Summary
Partitive division problems tell you how much total, and how many groups to share that total among. The question asks for how many in 1 (each) group. Partition division problems usually take longer to direct model, and are harder to figure out by counting than measurement division problems, though they are no more difficult than measurement problems for a student who knows their multiplication facts.
Measurement division problems tell you how much total, and how much is in 1 (each) group. The question asks for how many groups their are. Measurement division problems can be solved by skip counting up to the total or by subtracting the same amount repeatedly from the total.