Length

Lesson 6.1: Early concepts in measurement: Length measurement with standard and non-standard units.

Early measurement concepts

CCSS.Math.Content.K.MD.A.1: Describe measurable attributes of objects, such as length or weight. Describe several measurable attributes of a single object.

The first measurement concept that we need to help children develop is the notion that we can compare things by measurable attributes: we can say which of two things is taller, wider, longer, heavier or holds more (for example, which cup holds more water). We give examples and ask questions to explain clarify attributes that we can measure: height, length, weight, capacity. There are lots of things in a classroom that can be compared and measured, and there are children's books (like Measuring Penny) that can give children experience with describing and comparing objects.

Length

The main focus for measurement for grades K-2 is length (including height, width and length around an object). Length is particularly easy to show and explain and for children to understand.

In Kindergarten, children are expected to compare lengths directly:

CCSS.Math.Content.K.MD.A.2 Directly compare two objects with a measurable attribute in common, to see which object has "more of"/"less of" the attribute, and describe the difference. For example, directly compare the heights of two children and describe one child as taller/shorter.

Alice is taller than Bob

The apple is heavier than the banana

The first of the first grade length measurement standards builds on the Kindergarten skill to have children order 3 (or more) objects by their height or length. This standard explicitly includes using an object twice to provide a comparison of two objects that are not side by side:

Bob is shorter than Chris, who is shorter than Donna.

Bob is taller than Elaine, who is in his class at school.
Bob is shorter than the garden gate at his house.
That means Elaine must be shorter than the gate too.

Repeated (non-standard) units:

A main focus of length measurement in first grade is measuring objects using repeated units. That means you choose a small object and either use several of them, or use the same object several times to tell how long a longer object is.

CCSS.Math.Content.1.MD.A.2 Express the length of an object as a whole number of length units, by laying multiple copies of a shorter object (the length unit) end to end; understand that the length measurement of an object is the number of same-size length units that span it with no gaps or overlaps. Limit to contexts where the object being measured is spanned by a whole number of length units with no gaps or overlaps.

Notice some important concepts in using repeated units:

The units must be the same size ("multiple copies of a shorter object (the length unit)", "same-size length units")
The units must be joined end-to-end with no gaps or overlaps

These are important ideas for understanding measurement, whether you're measuring with paper clips or inches.

Using repeated small units also helps children build understanding of what a unit is when you are measuring, and it provides opportunities to build a sense of conservation of measurement. You won't find conservation of measurement specifically cited in the standards, but it's one of the basic ideas you need for understanding number and measurement. Some examples of important conservation of amount ideas are:

Conservation of number

Conservation of number: there are the same number of bear counters when they are spread out or grouped together

Conservation of length

Conservation of length: a string stays the same length when it is stretched out or bent

Conservation of volume: there is the same amount of water whichever container it is in.

Children gain understanding of conservation ideas as they grow, and also as they gain experience with number, length and volume. This means that informal tasks of pouring and measuring liquids (for example in cooking) are important as well as formal tasks of counging and measuring lengths.

In first grade, children learn to measure lengths (both straight and curved) using units that they repeat over and over. This can be a process of using lots of identical units (lots of paper clips) or using the same unit over and over (measuring the distance to the door by counting your steps as you walk heel-toe).

A "non-standard" unit is called non-standard because it is based on a convenient object rather than a standard length like an inch or centimeter.

Standard measurements and measuring tools

In second grade, students should also be measuring with standard units and standard measurement tools.

CCSS.Math.Content.2.MD.A.1 Measure the length of an object by selecting and using appropriate tools such as rulers, yardsticks, meter sticks, and measuring tapes

Experience with repeating non-standard units helps children undertstand that...

The inches or centimeters on a ruler are the distances between the measurement lines (the unit lengths are the distances, not the lines),
It's important to line up one end of your shape with the beginning of a measurement unit when you start measuring.

CCSS.Math.Content.2.MD.A.2 Measure the length of an object twice, using length units of different lengths for the two measurements; describe how the two measurements relate to the size of the unit chosen.

Measuring with larger and smaller non-standard units also prepares students for understanding how different standard units will give different numerical measurements: if the measurement unit is smaller (centimeters), it will take more of that unit (centimeters) to measure an object than it will if the measurement unit is larger (inches).

How Big is a Foot? is a fun story for discussing how it's important to know what the measurement unit size is in order to know how long something is.

In the book A Collection of Math Lessons Grades 1-3, Marilyn Burns and Bonnie Tank describe a lesson where children measure objects using Cuisenaire rods of different sizes and reason about how the number of yellow rods compares to the number of orange rods needed to measure something (this is a multiplicative or ratio relationship)

Estimating Lengths

CCSS.Math.Content.2.MD.A.3 Estimate lengths using units of inches, feet, centimeters, and meters.

The skill of estimating lengths has several sub-tasks.

Learning benchmarks for some standard length units. These can be benchmarks for just one unit (compare your thumb to an inch) or they can be benchmarks for several units (a standard sized piece of paper is 8 1/2 x 11 inches).
Comparing sizes: how many of your benchmark unit will fit into the length you're trying to estimate? For example, if a table is a little more than 4 pieces of paper long, you could estimate it's length at about 4 feet. Practice measuring with non-standard units can help with gaining this way of thinking about lengths.
Putting the numbers together (multiplication or addition): If your desk can just about fit 3 pieces of paper side by side, then its width is about 3x8 inches.
Checking for reasonable-ness: are you taller or shorter than the table is long? What does that tell you about how long the table can be?

Estimating puts together a lot of measurement skills--when done well, it's a complex task.

Measuring to compare:

CCSS.Math.Content.2.MD.A.4 Measure to determine how much longer one object is than another, expressing the length difference in terms of a standard length unit.

CCSS.Math.Content.2.MD.B.5 Use addition and subtraction within 100 to solve word problems involving lengths that are given in the same units, e.g., by using drawings (such as drawings of rulers) and equations with a symbol for the unknown number to represent the problem.

Measuring is a rich source of mathematical problems to solve. In second grade, children are explicitly expected to use measurements to tell how much longer one object is than another, and to solve other addition and subtraction word problems with measurements.

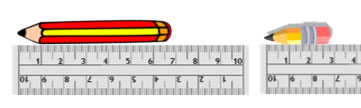
Janet's pencil is 7 cm long.
Paul's pencil is 3 cm long.
How much longer is Janet's pencil than Paul's?

Matt had 8 inches of bubble tape.
He chewed 3 inches of his bubble tape.
How much bubble tape does he have left?

Alice walked 52 yards.
Then she walked 26 more yards.
How far did she walk in all?

I think it's interesting that it seems to be easier to write sensible measurement word problems that are compare or take away problems than it is to write Part-Part-Whole or Join problems: comparing lengths is a reasonable thing to do in lots of situations; cutting off a length from a longer length is a reasonable thing to do, but putting two lengths together is something that you don't often do except, perhaps, with distances travelled.

Number lines as a continuation of measurement ideas:

CCSS.Math.Content.2.MD.B.6 Represent whole numbers as lengths from 0 on a number line diagram with equally spaced points corresponding to the numbers 0, 1, 2, ..., and represent whole-number sums and differences within 100 on a number line diagram.

Number lines are specifically mentioned in the section on measurement for second grade. Using a number line is often a great way to see word problems involving distance and length. In this measurement context, we try to be more careful with the spacing on the number line.

When we use number lines for addition and subtraction, often the focus is on composing and decomposing numbers, so while relative position is important (bigger numbers to the right of smaller numbers), it's not very important that the number line scale be perfect.

When we use number lines to represent measurement units, we try to have the units have a more consistent spacing, because measurement units always need consistent spacing.

Jack walked 4 blocks. Then he walked 3 more blocks. How many blocks did he walk in all?

Addition on a number line is shown with one or more arrows going up: often there is an arrow from 0 to the first addend. Always there is an arrow going up from the first addend with the length of the second addend

Sam had 6 feet of string. He cut off 2 feet of string to make a fishing pole for a skit. How much string does he have left?

One way to show subtraction on a number line is with an arrow going backwards. Often there is an arrow from 0 to the minuend (total). Then there is an arrow from the minuend back with the length of the subtrahend to show how much is taken away.

Andrea has a pink ribbon that is 7 inches long, and blue ribbon that is 4 inches long. How much longer is the pink ribbon than the blue ribbon?

Another way to show subtraction uses something like a compare idea. An arrow shows the difference starting at the subtrahend and going up to the minuend. The difference between the two values is the length of the arrow

The biggest of the big ideas about length measurement are:

You need a consistent unit length repeated over and over to measure how long something is. (grade 1)
When you repeat a unit, you should try to have no gaps and no overlaps (grade 1)
A standard length unit helps you tell someone else what a length is because everyone understands the unit (grade 2)
When you measure something you are counting lengths: on a ruler the inches or centimeters are the lengths between lines (grade 2)
When you measure with a ruler or other measuring tool, you need to be careful to line up your tool at one end of the object. (grade 2)
If you measure with a larger unit, you will need fewer units than if you measure with a small unit.(grade 2)
If you know how two measurement units compare, you can figure out how the number of units of each you need will compare. (Changing measurement units is best done with multiplication, so this one is a 4th grade standard)