
The third grade standards include several that are called "geometric measurement" standards. This refers to area and perimeter (and other similar concepts in higher grades): measurement attributes that are typically found by calculating something, rather than by directly measuring it. So areas are often broken down into simpler shapes (like rectangles), and the area is found by multiplying length measurements and adding it up. A perimeter is usually found by adding up side lengths. We use geometric reasoning, adding and multiplying of some length measurements to figure out other measurements.
The first, most basic idea of area is to understand that it is the amount inside a shape that's drawn on something like a piece of paper ("plane figure means that it's drawn on a plane).
With length measurement, we think of having a length unit (inch, centimeter, paper clip) that we repeat over and over to tell a total length. With an area measurement, we need an area unit that we repeat to get the total area. If you make a square each of whose sides is 1 unit long, then the area of that square is called 1 square unit. For example, a square that is 1 cm on each side has area 1 square cm = 1 cm2. When we repeat that unit, we want to cover or fill the inside of a shape with unit squares. Just like with length measurement, we want to fill it carefully, so the squares don't have gaps and don't overlap.

As children are developing an understanding of what area is, they should have experiences where they use appropriate materials (square tiles and grid paper) to practice finding area by counting unit squares.
Geometric measurement: understand concepts of area and relate area to multiplication and to addition.
CCSS.Math.Content.3.MD.6. Measure areas by counting unit squares (square cm, square m, square in, square ft, and improvised units). |
The big connection for third grade mathematics is between area and multiplication. As we saw in the lessons on multiplication models and properties, one important way to represent multiplication is with a rectangular array. That array picture corresponds to how square units fill up the area of a rectangle with a whole number of sides.
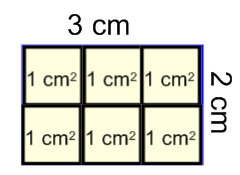
As a basis for understanding this connection between multiplication and rectangles, children should have experiences where they can both count and multiply to find the area in square units.
This is such an important way of understanding multiplication, that we want children to be able to go back and forth between multiplication and rectangle pictures. For example:
If the question is: find the area of a rectangle that is 2 cm high and 3 cm wide
We want the learner to: recognize that it has 2 sets of 3 square cm, so the problem can be solved by multiplying: 2 × 3 = 6 square cm. (first part of b)If the question is: multiply 2x3
We want the learner to: recognize that one picture they could draw to show 2x3 is a picture of a rectangle that is 2 high and 3 wide (second part of b)
(Side note: this process of going back and forth between a situation and picture with a rectangle and a numerical multiplication problem is an example of contextualizing and decontextualizing a problem, and of using mathematics to model a situation (like area)--see the CCSS Practice Standards 2 and 4).
Two important number ideas that are easier to show when you draw them with a rectangle are the commutative law and the distributive law. The common core standards (7c) specifically describes the connection that learners should be making by using rectangles to illustrate the distributive law:
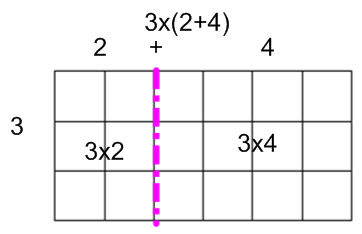
One of the ideas you need to make sense of this distributive law picture is stated again in part d of this standard: area is additive. This means you can break up a larger shape into pieces, and if you find the areas of the smaller pieces, you can add them together to find the area of the whole thing. In third grade, children should be doing this with shapes that are easy to decompose (break down) into rectangles.
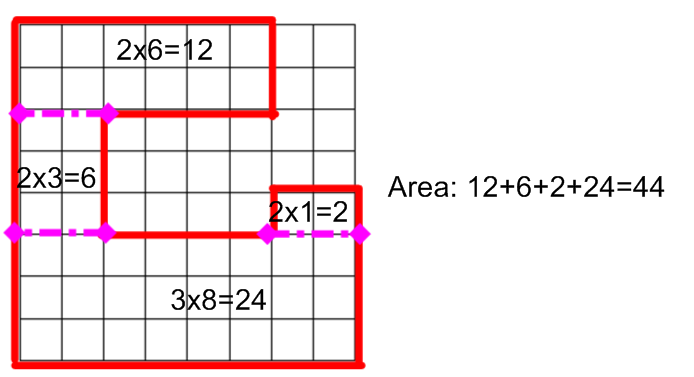
Geometric measurement: understand concepts of area and relate area to multiplication and to addition. CCSS.Math.Content.3.MD.7. Relate area to the operations of multiplication and addition.
|
The perimeter is the distance around a shape, It's a length measurement. Because it's a measurement of a 2-dimensional shape, it's important to keep track of the difference between perimeter (length units) and area (square units).
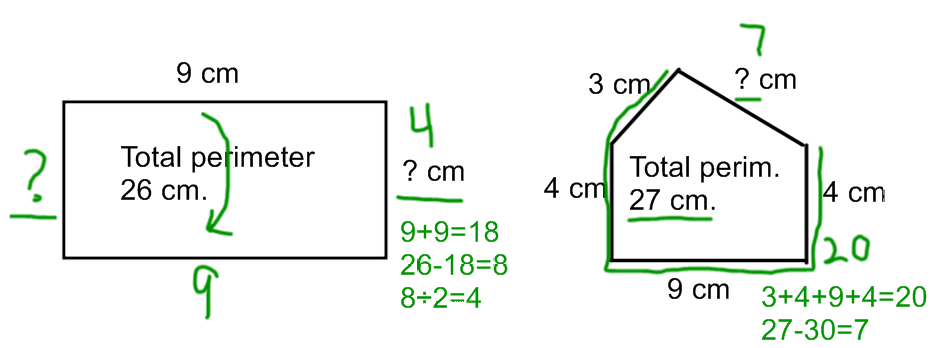
Perimeter problems in third grade include:
Adding up side lengths to find the perimeter:
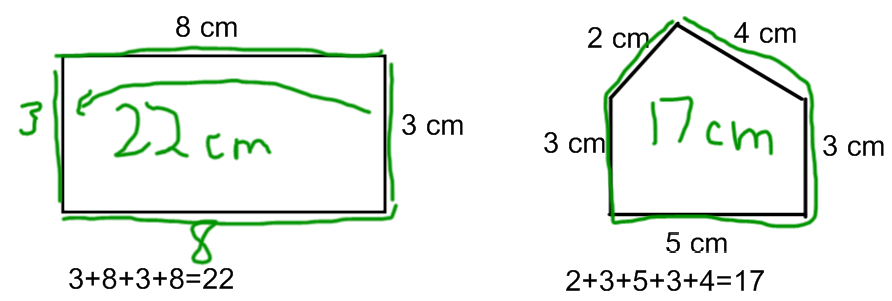
Using the perimeter to find a missing side length:
Building rectangles that have the same perimeter, and different areas (each of these rectangles is made from 12 matchsticks. By using the same length manipulative, I make sure the rectangles have the same perimeter.)
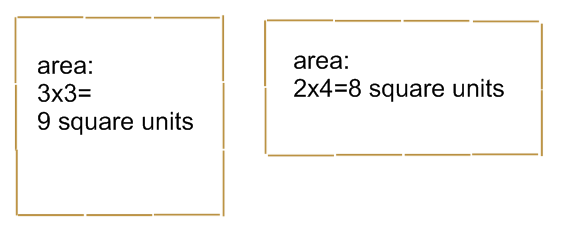
Building rectangles that have the same area, and different perimeters (each of these rectangles is built from 12 square centimeters. By using the same area manipulatives, I make sure the rectangles have the same area):
