Named geometric shapes like triangles, rectangles and circles are specific shapes with geometric properties. Developmentally, children first learn to recgnize and name shapes by looking at examples. Later, children learn properties such as "having straight sides" or " having square corners", and use them to describe shapes.
Many properties children identiry are informal (horizontal, pointy, looks like a ...) and measurement oriented (large or small). The more formal, geometric properties that children learn to recognize are ones that don't depend on the overall size or orientation of the shape (parallel sides, equal sides, right angles). Learning about shapes and properties is both developmental and instructional--the choice to study shapes in a way that doesn't depend on their size and orientation is a fundamental one to how geometry is organized. Definitions of special shapes (such as rectangles) are given as a list of properties that the shapes have. As children study geometry, they learn to figure out when a set of properties defines a shape, and how to describe properties more carefully. Attribute is another word for property in geometry.
Dina and Pierre Van Hiele studied how children thought about and understood shapes and geometry. they categorized students understanding into several levels. We're going to be most interested in levels 0, 1 and 2.
Level 0: Visualization
Children start out at a visualization level of understanding geometry and thinking about shapes. Visualization is holistic: children identify shapes by recognizing that they look like examples they have seen. When they describe shapes, they use informal comparisons (it looks like a mountain or a house or a kite), descriptions that use non-geometric properties (it's blue or green or orange), and often attach importance to the orientation and size of the shape (flat on the bottom, diagonal, small).
Level 1: Analysis
Children learn to analyze specific shapes and groups of shapes to find geometric properties. As children move from a level 0 to a level 1 understanding, they learn to recognize common geometric properties by name (straight sides, right angles, equal sides), and they learn that properties that don't depend on orientation or overall size are more important than position and orientation properties. Children at the analysis stage can not only identify whether a property is true of a particular shape (children at level 0 can also do this), but can also identify whether a property is true of all of the shapes in a known group (for instance--do all squares have line symmetry?)
Children at this level may describe and define a shape by listing a lot of the properties that the shape has (parallelograms have opposite sides that are parellel and have the same length, their opposite corners have the same angle).
Children can, with appropriate instruction, gain an analysis level of understanding of shapes in the primary grades (1, 2 and/or 3)
Level 2: Informal deduction.
Children who engage in informal deduction use properties of shapes to deduce relationships between shapes (for example, a square is a specific kind of parallelogram because its opposite sides are parallel). Definitions at this level can be more concise (for example, every 4-sided polygon with opposite parallel sides is a parallelogram, so equal sides doesn't need to be included in the definition).
Moving from level 0 to level 1: Sorting shapes into groups by properties. . In this activity, children are provided with a variety of shapes, and asked to sort them to make a group of shapes that are all the same in some way. This activity is discussed in more detail in the Van de Walle text: Teaching Student Centered Mathematics
The teacher should also teach mathematical vocabulary (parallel, equal, right, acute, obtuse) in combination with repeated opportunities to sort and describe groups of shapes.
The description of the groups in a shape sorting activity can reflect the level of geometric thinking that was used for the shape sorting:
Level 0 descriptions often have orientation or visual similarity cited as sorting rules |
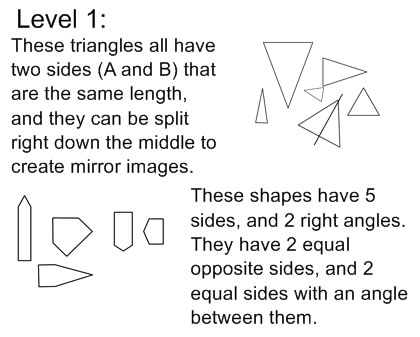
Level 1 descriptions often have a lot of properties listed (more than are needed) |
Level 2 descriptions often have more efficient lists of properties. The descriptions are usually more careful and include more mathematical vocabulary. |
Deepening level 1 and moving to level 2 understanding: Guess my rule is an activity where children try to guess the rule that produced a particular group or sorting of shapes. This task strengthens students understanding of what rules can be used to define a set of shapes. It helps students move from level 1 to level 2 by focusing their attention on the properties needed to define a group:
| Standard | Comments |
| CCSS.Math.Content.K.G.A.2 Correctly name shapes regardless of their orientations or overall size | This specifically addresses childrens' common misconceptions especially about triangles and squares. Children don't need to be at level 1 to correctly name shapes, but they do need visualizations that include lots of variety so that their notion of what a triangle "looks like" matches the geometry definition of a triangle. (lv 0) |
| CCSS.Math.Content.K.G.B.4 Analyze and compare two- and three-dimensional shapes, in different sizes and orientations, using informal language to describe their similarities, differences, parts (e.g., number of sides and vertices/“corners”) and other attributes (e.g., having sides of equal length). | This specifies that children in kindergarten are expected to do work where they look for and describe properties of specific shapes. It implies that children should be starting to do activities like the shape sorting task described above that are intended to encourage level 1 thinking, though without the goal of using standard vocabulary. (lv 0-1) |
| CCSS.Math.Content.1.G.A.1 Distinguish between defining attributes (e.g., triangles are closed and three-sided) versus non-defining attributes (e.g., color, orientation, overall size); build and draw shapes to possess defining attributes. | This implies two things: Children will learn definitions of specific, common shapes, and will be able to use those definitions to identify and draw examples of those shapes. Children will have enough experience with geometry definitions that they know what sorts of attributes are used in geometry definitions, and what sort aren't considered important properties of shapes. (lv 1) |
| CCSS.Math.Content.2.G.A.1 Recognize and draw shapes having specified attributes, such as a given number of angles or a given number of equal faces.1 Identify triangles, quadrilaterals, pentagons, hexagons, and cubes. | This standard gives a list of some shapes children should know and have a mental image of that matches the standard definition. (lv. 0) This standard also specifies that children should have experience in reasoning from properties to come up with examples that match the definition. (lv 1) |
| CCSS.Math.Content.3.G.A.1 Understand that shapes in different categories (e.g., rhombuses, rectangles, and others) may share attributes (e.g., having four sides), and that the shared attributes can define a larger category (e.g., quadrilaterals). Recognize rhombuses, rectangles, and squares as examples of quadrilaterals, and draw examples of quadrilaterals that do not belong to any of these subcategories. | This standard says that children need to understand that some shapes are subsets of other shapes, and it gives some specific examples of subsets children need to know (rectangles are quadrilaterals, etc.) (lv 1-2) This standard also says that children should know how that subset relationship works with shared attributes. (lv 1-2) |
If you compare this to what Van de Walle describes as what children usually understand at these grade levels, you'll see that the Common Core is pretty ambitious in terms of student understanding of geometry at these grade levels. In the next few years, elementary teachers will need to think about what they do in geometry at these grade levels, and whether it is robust enough to support what the Common Core is expecting children to learn.
Kindergarten:
Providing and discussing a variety of examples of standard shapes can help children understand shapes better. Being able to recognize shapes in unusual orientations and examples is (as you saw in the earlier lesson on triangles, squares and rectangles) tricky for some children. I'm not sure how common it is (a student in this class in a previous year tried it out with her pre-schoolers, and they didn't have any trouble at all!), but it's an issue that as a teacher you need to be aware of. Include tricky triangles in your pre-assessments to find out what children know. If children have trouble with tricky triangles or tilted squares (or maybe even if they don't show misconceptions), make sure you include some tricky examples when you talk about shapes. Knowing a variety of examples of standard shapes helps children build geometry understanding and inutition.
Ask about properties of shapes. Knowing that properties are important is something children learn by discussing and working with properties. Children at the visualization level can insepect specific examples of shapes and figure out what properties they have. By asking good questions, you help children learn what geometric properties are. Asking good questions means asking children whether shapes have specific geometric properties like: how many sides does it have? Are the sides the same length? Are the corners square? As the teacher, you know what properties are more geometric (number of sides, number of corners/angles, size of corners/angles, symmetry, etc), what properties are measurement properties (which is larger? How long is it? How tall?), and what properties are non-mathematical (what color is it?). By asking geometric and mathematical questions you are teaching children to look for geometric properties, and you are teaching that these are important properties when you are thinking about shapes.
First grade
Preassess It would be nice to think that all children entering first grade would have an accurate understanding of basic shapes and properties. That sounds a lot like wishful thinking, however. Listen to the children so you know what they know and what they don't know yet.
Defining attributes are the attributes that are important in the definition of the shape--they are the properties that make a triangle a triangle, and a rectangle a rectangle. The most basic things you can do to help children understand this distinction are to discuss definitions: a rectangle is a shape that..., a triangle is a shape that.... what makes a square a square? Children should practice sorting things that fit the definitions from things that do not: in a set of tricky triangles (or rectangles or ...), sort the set into shapes that are triangles and shapes that are not triangles (or rectangles or ...). Children should also practice drawing things that fit the definitions and things that do not: draw a shape with 4 sides that is not a rectangle.
Looking for and sorting shapes by properties also provides good opportunities to teach important properties and vocabulary, and children gain practice and familiarity with thinking about shapes by thinking about their properties.
Second grade
Preassess: See comments on first grade. Look for understandings and potential misconceptions.
Give good examples of shapes to sort by given attributes. When you're looking for a set of shapes, think about what might be tricky about an attribute (For example right angles are harder to see if they aren't horizontal and vertical--if your sorting attributes include right angles, you want some tilted ones in your sorting set).
Drawing shapes with given attributes is easiest if you're just trying to draw something with one given attribute, and it gets more complex when you have more attributes you're trying to match simultaneously (drawing an isosceles triangle is easier than drawing an obtuse isosceles triangle). Plan a progression from easier to harder, and plan on discussins about how students figured out tricky problems.
Include shape sorting or other activities with a wide variety of shapes--lots and lots of shape examples. When you're trying to think of whether a shape could have two properties at the same time (like obtuse and isosceles), it helps a lot if you're seen shapes that have both of those properties before.
Third grade
Preassess: See comments on first grade. Look for understandings and potential misconceptions.
Third graders are expected to work with relationships between types of shapes. The examples in standard 3.G.A.1 uses the example that squares are a type of quadrilateral. This is a comparitively easy one for children to accept: understanding that a new type of shape (quadrilaterals) is inclusive of other shapes (squares, rectangles) is easier to fit into their mental framework than changing their mental definition of rectangles to include that squares are special kinds of rectangles.
Shape sorting with tricky shapes is one way to approach the big idea in this third grade geometry standard. The big idea is that shapes can be subsets of other more general shapes. Shape sorting in this context involves defining a set by a property (4 sides or 2 parallel sets of sides or 4 right angles) and having children sort shapes as belonging or not belonging to that set. The shapes to be sorted should include shapes that might be problematic (squares, rectangles, etc). This should result in squares being included in the rectangle group (4 right angles) and rectangles and squares being sorted in the parallelogram group (2 parallel sets of sides) etc. I would recommend initially starting with sorting by property and not by name, and attaching the name to the group after sorting (this means that children focus on the property and aren't distracted by their visual examples of the named group).
Set diagrams are helpful for showing relationships between different kinds of shapes. It helps to include, and have children include, drawings of examples in the set diagrams.
