This lesson is all about vocabulary. Hopefully, these are all terms that you knew before, and I'm just reminding you and refreshing your memory.
Triangles can be classified by angle size into acute triangles, right triangle and obtuse triangles

| An acute triangle is a triangle where all of the angles are acute. OR An acute triangle is a triangle where the largest angle is acute |
A right triangle is a triangle where one of the angles is a right angle. OR A right triangle is a triangle where the largest angle is a right angle |
An obtuse triangle is a triangle where one of the angles is obtuse. OR An obtuse triangle is a triangle where the largest angle is obtuse |
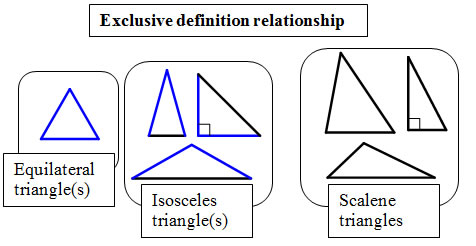
Triangles can be classified by how many sides are congruent. There are two different ways you might find triangles classified:
Scalene always means that all of the side lengths are different.
Equilateral always means that all of the side lengths are the same.
Isosceles sometimes means that at least two of the side lengths are the same, and it sometimes means that exactly two of the side lengths are the same: there's an inclusive and an exclusive version of the definition. I wonder which definition you'll find at your school?

Each triangle can be sorted both by their side lengths and by their angle measures
The Montessori "7-triangles of reality" work involves sorting the triangles in both ways simultaneously into a grid. The children trace the triangles into the grid. In the Montessori work, they use the exclusive definition for isosceles, so the grid looks like this:
| Acute | Right | Obtuse | |
| Scalene |  |
 |
 |
| Isosceles |  |
 |
|
| Equlateral |  |
Polygons that have 4 sides are quadrilaterals. There are even more named varieties of quadrilaterals than there are varieties of triangles.
Parallelograms: One property that quadrilaterals can have is that they can have parallel opposite sides. If each side has a parallel opposite side (two pairs of parallel sides), the shape can be called a parallelogram. Rectangles, squares and rhombi (rhombuses) are parallelograms because their opposite sides are always parallel. It's also correct to say that a quadrilateral is a parallelogram if its opposite sides are the same length, but usually in the definition we use that the opposite sides are parallel because the word parallel is part of parallelogram.

Rhombus
A rhombus is any quadrilateral that has all 4 sides equal length. A rhombus can look like a diamond or a square or maybe a parallelogram (with all sides equal length).

Rectangle
A rectangle can be defined as a quadrilateral with all 4 right angles. It's also true that rectangles have two pairs of opposite, equal, parallel sides, but you don't need that in the definition. Having 4 right angles is enough.

Square
A square can be defined as a quadrilateral with all 4 right angles and all 4 equal sides. You can also define it as a rectangle with equal sides or a rhombus with right angles. That means a square is a special kind of rectangle and a special kind of rhombus.


Trapezoid: Trapezoid has two definitions: an inclusive and an exclusive definition. Quadrilaterals that have one pair of parallel sides are called trapezoids. M, N and U are all trapezoids. Some math books (and lots of mathematicians) say that a trapezoid has at least on pair of parallel sides (inclusive), so that would make a parallelogram (with two pairs of parallel sides like K, O, P and Q) just a special kind of a trapezoid. Other math books (including most of the high school geometry books I've looked at recently) say that trapezoids have one and only one pair of parallel sides (exclusive). Both definitions are right in different contexts.


Kite: Sometimes we give special names to other shapes too. There are shapes called kites. The definition of kite always includes something like: a quadrilateral that has two pairs of adjacent sides. There are actually 4 different variations on the meaning of kite that you might find in a math book, depending on whether all 4 sides can be equal or not (inclusive/exclusive), and whether you want to insist that it has to be convex. My examples here show the most inclusive definition of kite.

Every triangle can be classified by its angles and by its side lengths, but there are some quadrilaterals that don't have any special classification at all. These quadrilaterals don't have any special name:

Relationships: One important idea about classifying shapes is that the same shape can fit into more than one category, and some categories are subsets of other categories. For example:
| A square is a special kind of rectangle. All squares are rectangles. Some rectangles are squares, and some rectangles are not squares. | 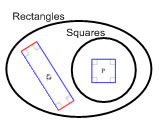 |
| A square is also a special kind of a rhombus. All squares are rhombi (or rhombuses). Some rhombi are squares, and some are not squares. | 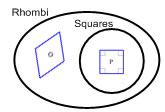 |
| A square is a rectangle and also a rhombus. Everything that is both a rectangle (90° angles) and a rhombus (all equal sides) is a square. | 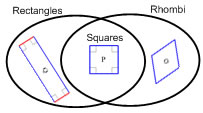 |
| Squares, rectangles and rhombi all have parallel sides, so they are all parallelograms. There are some parallelograms that don't fit rectangles, rhombi or squares. | 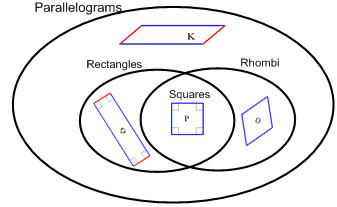 |
All of these shapes (as well as trapezoids, kites, and a few others) are quadrilaterals because they all have 4 sides.
Pentagons are polygons with 5 sides
|
Hexagons are polygons with 6 sides
|
| Hepagons have 7 sides | Octagons have 8 sides |
| Nonagons have 9 sides (cute video) | Decagons have 10 sides |
The more sides you get, the less likely it is that is will have a name. 12 sides is a dodecagon. After that I don't know any other names. Polygons with more sides can all be named using their number: 12-gon, 15-gon, 22-gon etc.
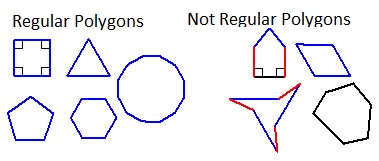
Regular Polygons whose angles are all the same and whose sides are all the same are called regular polygons. It's possible to have polygons with equal sides and unequal angles and vice versa, so it's important to have both conditions. The pictures you find of shapes are usually pictures of regular polygons