
One of the ways of using geometric shapes is by putting together several simple shapes to make a more complex shape (composing shapes) and by splitting a shape up into simpler shapes or splitting it in a systematic way to make new shapes.
In kindergarten, children are expected to compose simpler shapes to make more complicated shapes:
K.G.6. Compose simple shapes to form larger shapes. For example, “Can you join these two triangles with full sides touching to make a rectangle?”
| Children naturally will use pattern block shapes to make pictures and designs, and that experience helps build understanding for how shapes can be put together. |  |
| A more focused exploration might ask: how many different shapes can you make from 4 pattern block triangles? By insisting that blocks have to touch on a full side, you both restrict the number of shapes that can be made, and you build into the activity a component of thinking about side length properties. |  |
Another good question might be how many different rectangles (and squares) can you make from tangram shapes?
Tangrams are triangle, square and parallelogram shapes in a particular size ratio to one another.
If you follow the pattern shown in the square on the left, you can make tangram shapes from any square. Using just a few tans (tangram shapes) at a time, you can make different sizes of squares and other rectangles.
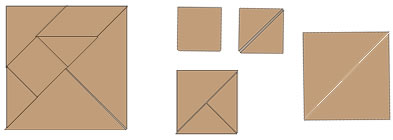
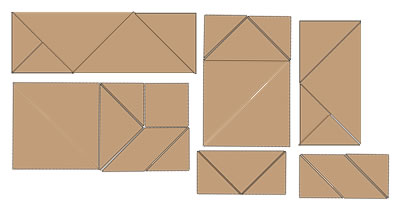
There are a lot of tangram rectangles, and I don't think I've found them all. By trying to make rectangles rather than just any cool design, the activity includes ideas of looking at properties of angles and side lengths.
The common core standards focus in on just two specific ways of decomposing shapes--splitting them into smaller shapes. One of these focus ideas is using decomposition to understand fractions, and the other is using decomposition s to understand area.
It's interesting to note that the geometric notion of a fraction is emphasized in the common core standards above any interpretations of a fraction as part of a set. Finding a fraction of a set (how much is 1/4 of 12, for instance) isn't specifically included in the standards at all, and isn't even implied as a learning goal until grade 4. It will be interesting to see how this affects future textbooks and assessments (currently it is often included in second grade).
The geometric notion of a fraction consists of splitting a shape (circle, square or rectangle) into equal parts, and using those equal parts to represent the fraction.
1.G.3 Partition circles and rectangles into two and four equal shares, describe the shares using the words halves, fourths, and quarters, and use the phrases half of, fourth of, and quarter of. Describe the whole as two of, or four of the shares. Understand for these examples that decomposing into more equal shares creates smaller shares.
2.G.3. Partition circles and rectangles into two, three, or four equal shares, describe the shares using the words halves, thirds, half of, a third of, etc., and describe the whole as two halves, three thirds, four fourths. Recognize that equal shares of identical wholes need not have the same shape.
3.G.2 Partition shapes into parts with equal areas. Express the area of each part as a unit fraction of the whole. For example, partition a shape into 4 parts with equal area, and describe the area of each part as 1/4 of the area of the shape.
If you look at these standards from grades 1, 2, and 3, you should notice that:
The easiest fraction to understand is halves. We use the word half for sharing into two pieces in our everyday language. Fourths are the next easiest to understand--half of a half. Geometrically, children learn about halves and quarters by drawing, folding and cutting.
Understanding that the size of the pieces are smaller when you cut into more pieces is easy to see with halves and quarters because you generally aren't cutting into quarters independently of halves--you go through the process of first dividing into halves, and then dividing each half into halves to get quarters.
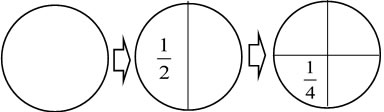
Because it's important that each piece be exactly the same size, there's only one easy way to partition a circle into 4 equal pieces, but it turns out that there are a lot more ways of partitioning a square or a rectangle.

It's not easy, at first, for children to see and believe that all of these fourths--even the ones that are different shapes--are all the same size. They have to be the same size, of course, because they are all 1/4 of the same sized whole, but that's a tricky thing to understand and believe and it takes time to get used to the idea. You see this idea showing up in the second grade standard, and again, in terms of area in the third grade standard.
Area shows up in two different ways in the geometry standards:
2.G.2 Partition a rectangle into rows and columns of same-size squares and count to find the total number of them.
3.G.2 Partition shapes into parts with equal areas. Express the area of each part as a unit fraction of the whole. For example, partition a shape into 4 parts with equal area, and describe the area of each part as 1/4 of the area of the shape.
Partitioning a rectangle (or anything else) into squares of unit size is the most basic way to think about area: the area of a shape is the number of unit squares covered or enclosed by the shape. Now, partitioning into squares can be tricky: it's easy when you're first starting out to loose track of your squares, so there are some advantages to first exploring with unit square manipulatives that can be used to physically fill or cover your shape, or to trace shapes onto grid paper.

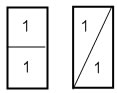
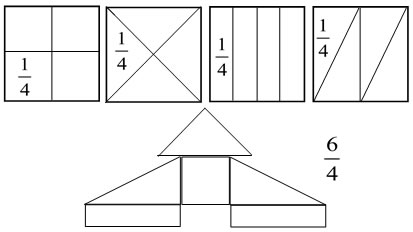
The other big idea is that you can find areas of fractional parts by comparing to the whole. That means that each of these shapes has area that is 1/4 of the area of the square, so that composite shape has area 6/4.
It also means that if you know a rectangle has area 2, then half of the rectangle has area 1: