Solutions to practice problems
1. Cut out 2 identical scalene right triangles. How many different shapes is it possible to make by putting the triangles together in a way that sides match up perfectly with sides?
There are only 6 possible ways to match 2 scalene right triangles:

2. Suppose you had a set of 8 of identical scalene right triangles for each student or pair of students. What would be an assignment that would get students to focus on side lengths and angles?
Possible answers:
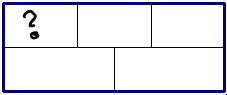
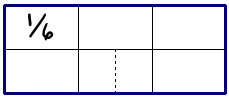
3. Tricky fraction picture--if the whole rectangle shows 1, what fraction size is the part with the "?"?
This is a tricky picture because the 5 pieces have different sides, so this isn't a partition into fifths. However, the top half is split evenly, and you can see that if you did the same thing on the bottom you would have 6 equal parts, so this part shows 1/6:
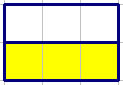
4.. Explain how to use fractions to find the area of this triangle:
Answer #1: The triangle has half of the area of the rectangle, and the rectangle has area 6 square units, so the triangle has area half of 6 square units, so its area is 3 square units.

Answer #2: Both of these are ways of splitting the rectangle in half. Beacuse both shapes show half of the same rectangle, the shapes must have the same area. The area of the yellow rectangle is 3, so the area of the yellow triangle must be 3.