
1. Look at these sample answers to a problem about making fractions on a geoboard (from Everyday Mathematics grade 3)
a. Tell what fractions are shown in each diagram
top left: 1/12's, top right: 1/3's
bottom left: 1/3's, bottom right: 1/6's
b. How could you prove that the parts shown in each diagram are equal?
top left: each is a single square, and all of the squares are the same size
bottom left: each is a rectangle, and all of the rectangles are the same size (each rectangle is 4 squares)
top right: each piece contains 4 squares
bottom right: the bottom two rectangles have 2 squares each. Each of the triangles can be split into 2 smaller triangles that can be put together to make a rectangle that covers 2 squares, so each triangle has an area of 2 squares:
c. In what ways are the two diagrams on the right different from the diagrams on the left?
The ones on the left have pieces that are the same shape and size. The ones on the right have pieces that are the same size, but not the same shape.
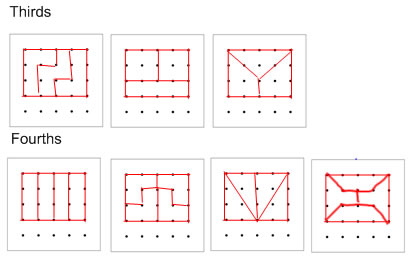
2. On your geoboard, or on geoboard dot paper, find several more ways of showing thirds and fourths on the same rectangle shown in the previous problem (4 spaces wide by 3 spaces high)
Many answers are possible, of course. Here are a few of mine:
3. What is a shape that it is hard to find different ways to divide it in half? What is a shape that it is easy to find different ways to divide it in half?
It's hard to find more than one way to divide a circle into a particular fraction (like a half). Rectangles and squares are much easier
4. If you use a yellow hexagon (from your pattern block set) to represent a whole, what fractions are easy to represent? What shapes would represent them?
Easy fractions are:
1/2: trapezoid
1/3: blue rhombus
1/6: triangle
5. Explain, using the same ideas emphasized in the grade 3 fraction standards, what 3/4 means. Draw a number-line diagram to help your explanation.
If you split a whole unit into 4 equal parts, then each of those parts has size 1/4. 3/4 means 3 parts, each of which has size 1/4.
6. Explain, using the same ideas emphasized in the grade 3 fraction standards, what 4/3 means. Draw a number-line diagram to help your explanation.
If you split a whole unit into 3 equal parts, then each of those parts has size 1/3. 4/3 means 4 parts, each of which has size 1/3.
7. Tell a fraction that is equivalent to 3/4. Draw a rectangle-diagram to help your explanation.
Split a rectangle into fourths using only horizontal lines, and shade in to show 3 parts of size 1/4. Then divide it with 1 vertical line down the middle. Now you have 6 shaded parts out of 8 equal parts in the whole. That means 3/4 and 6/8 show the same amount:
8. Tell a fraction that is equivalent to 3/4. Draw a number-line diagram to help your explanation.
Split a unit length into fourths, and put a dot at where 3/4 is on the number line.
Now split each of the fourths into 2 equal pieces. It takes 8 of those equal pieces to make 1 whole, so each of those show 1/8. Count up to the dot. that number is 6/8.
3/4 and 6/8 show the same dot on the number line, so they are equivalent fractions:
9. Tell a fraction that is equivalent to 2. Draw a number-line diagram to help your explanation.
There are many possible right answers. This is one of them:
6/3 = 2 because when if you split each unit into 3 equal parts (thirds) and count up, then there are 6 equal steps to get to 2.
10. Describe three different ways that children might solve the problem of 6 children sharing 8 brownies.
I'm hoping that everyone got these two ways of solving the problem:
There is one other solution strategy that would apply well to this problem:
Children will often move from giving out whole brownies to cutting each of the brownies in half, but that isn't as likely a strategy for this problem because splitting the two remaining brownies in half gives only 4 pieces, which is not enough for 6 children. It is likely that some children would try to solve the problem by cutting brownies in half, and then cutting the halves in half, but that strategy isn't likely to be successful for this problem.
11. Explain how to compare two fractions that have the same denominator. (Make sure you include the "why it works" not just the "how to do it")
If two fractions have the same denominator, that means that they are made out of the same size pieces. The one with the larger numerator has more pieces, so it is the larger fraction.
12. Explain how to compare two fractions that have the same numerator. (Make sure you include the "why it works" not just the "how to do it")
If two fractions have the same numerator, that means they are made out of the same number of pieces. If two fractions have a different denominator, then the one with the larger denominator has smaller sized pieces, because you need to cut the whole into more shares. The fraction whose pieces are larger will be bigger because there are the same number of pieces in both fractions. The fraction with the smaller denominator has larger pieces, so the fraction with the smaller denominator will be the larger fractional amount.