Cognitively Guided Instruction, Lesson 8:

Teaching addition and subtraction using word problems for students at the direct modeling stage.

This lesson tries to answer the question: how should I use my knowledge about addition and subtraction word problems when I'm teaching? In particular, this we'll be looking at what to do for children (probably K-1) who are confident with their counting abilities, but don't have a lot of experience and expertise with addition and subtraction. I'll discuss some important guiding principles, and share a sample lesson.

Three important principles for teaching children, and in particular, teaching with word problems and problem solving:

• Start with easier problem types and problems, and move on to more difficult problems as children become confident with the easier problems.
• Build on what they know--pay attention to what children know, and ask problems that they have the tools to solve.
• Understanding the problem is the most important step. Children should solve problems by first making sense of them.

Some discussion of the principles:

Start with easier problem types and problems, and move on to more difficult problems as children become confident with the easier problems.

The guiding principle here comes from Vygotsky, and the key phrase is "zone of proximal development". The idea is that children (and everyone) learns most when they are working problems of just the right difficulty. If it's too easy, then there's no real thinking involves, and thus not much learning. If the problems are too hard, then you can't solve them at all, and you don't learn anything. If the problems are just hard enough to be a challenge, but easy enough so that you can solve them confidently, then you're most likely to learn from the experience.

With children and math word problems, we want the problems to be just hard enough to require some real thinking, but not too hard so that children can't solve the problems. One way to tell if your problem is reasonable is to look at the numbers. If they child is at a stage where they solve problems by acting them out (direct modeling), then the key prior knowledge pieces are that they be able to confidently count as high as the numbers in the problem, and that they understand the problem well enough to figure out how to act it out. Experiences with easier problem types are helpful for children to have before they move on to harder (more confusing) problem types, because they gain skill in representing a problem in ways that let them solve it.

It's usually wise to start with very easy problems: simple Join, Result Unkown problems, with fairly small numbers. When the children show you that they are confident at solving problems like that, and the first sort of problem you started out with is easy for them, then it's time to move on to harder problems. A harder problem can be harder just because it's worded differently (see Lesson 5), it can be harder because it's a more difficult problem type, or it can be harder because the numbers are larger. It's a good idea to make the problem harder in only one way at a time (so either go to a harder problem type, or go to larger numbers, but don't try to do both at once). Usually it's wisest to start by making the number larger, and then when children show that they can solve a lot of problems of that type, with a reasonable range of numbers, then you can move on to the next problem type. The one exception to this is that Separate Result Unknown problems are not really any more difficult for children who are solving the problems by direct modeling, so you can safely work in some of those quite early on.

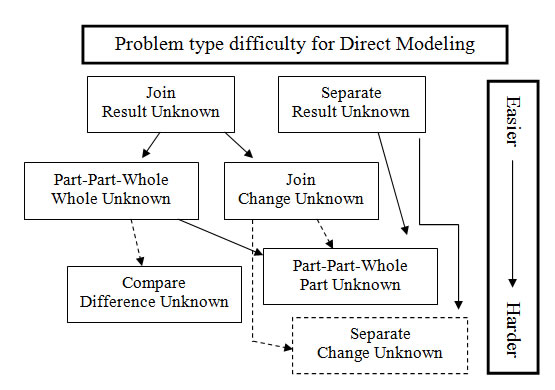
I think this is a good place for a problem type difficulty chart. This chart is designed to reflect what is easier or harder for children at the direct modeling stage of problem solving--we'll revisit this again when we look at counting and derived facts strategies.

Things to notice here:

• Join and Separate Result Unknown are both at the top, because they're both easy to direct model. All of the other problem types directly or indirectly are related to the Join Result Unknown problems.
• A child who is confident at solving JRU problems may be ready to be introduced to either Part-Part-Whole, Whole Unknown problems or to Join Change Unknown problems. Their experience with JRU problems will help them figure out, or will help them be ready to learn about the next problem types.
• Children need to be confident with understanding and solving Part-Part-Whole, Whole Unknown problems in order to understand and try to figure out Part-Part-Whole, Part Unknown problems. Experience with JCU and SRU problems will probably be helpful too.
• Children need to be confident with Separate, Result Unknown problems in order to be ready to try to solve Separate, Change Unknown problems. Separate, Change Unknown problems are less central to later math learning, and so if there's a problem type to skip and not worry about on this list, SCU is it.
• Children need to have some experience thinking about sets and comparing sets in order to be ready to learn about Compare, Difference Unknown problems. There isn't a particular problem type that supports learning about CDU problems, though experience in general is helpful. In an average class, you are likely to have some children who can spontaneously figure out how to model CDU problems, and you are likely to have some children who are confused by the problems. Having children share their strategies with the whole class may be particularly useful when introducing CDU problems.

Build on what they know--pay attention to what children know, and ask problems that they have the tools to solve.

One part of building on what they know is knowing how far the children can confidently count. If you are asking problems that fall within the range of numbers children can confidently count, then they can probably solve them by direct modeling. As children practice and expand how far they can count, you can raise the numbers accordingly.

Another part of building on what they know is being aware of the child's vocabulary and experiences. If you choose a context children are familiar with, and you use vocabulary they are comfortable with, children will be better able to visualize and figure out how to solve the problem. Be aware that not all children have the same background, and you may need to purposefully build vocabulary with children to include words they will need to know in school.

Knowing what problems they have successfully solved in the past can also help you make good choices. If you can take a problem they've been successful with, and build on it by making it a little harder, but still recognizably the same problem, then the children will have a good place to start in figuring out the new problem.

If you run into problems that children can't solve, try to look for the component pieces of knowledge that a child would need to be able to act out the problem in a direct modeling way. Look for pieces that are new to the children, and teach those pieces before you come back to that or a similar problem.

Understanding the problem is the most important step. Children should solve problems by first making sense of them.

This is true both if you are teaching addition and subtraction using word problems, and if children are doing any sort of problem solving. Children can figure out a lot of things if they can clearly understand what it is that you are asking. Indeed, one guage of whether a problem solving problem or exploration is at the right level for the child, is that they should be able to figure it out by themselves if they understand the problem well enough. When you are asking problems that are new (a new problem type, or other significant change), plan to invest some time in helping children make sense of the problem.

• A good place to start is to give the children some think-time after you tell the problem.
• Then, if several children are coming up with answers, then you can build on that by having them show how they solved the problem.
• If you think the problem is likely to be misunderstood (because of the wording of the problem, or because you have ELL students, or whatever), you might want to have children retell the problem to the class: their rewordings can be valuable for the whole class, and you can find out if they are understanding what you meant in the problem.
• If none of those strategies are working, it may be a sign that you should back up to some easier problems for a while, and try to come up with experiences you can build into other parts of your lessons to give children the background they need to be ready for that type of problem.
• It can be a good thing to show children with manipulatives or with a picture how you would direct model the problem--pictures and materials can be very helpful in explaining what a problem means. You and the children will both learn more, however, if you listen to what they children are thinking first.
• After the children and/or you have shown how to direct model the problem, be ready with another problem that is very similar so that children can follow up on what they heard and learned.

A Sample Lesson:

This is a 15-minute lesson with either the whole class or with small groups. This is an example of a lesson that introduces PPW-WU problems. A similar lesson that did not introduce a new problem type would last about 10 minutes. Doing a few problems daily on alternate days for these type of small problems is generally better than doing a lot of them for just a few weeks.

Children have counters, pencils and paper.

The teacher asks a JRU problem s/he is confident the children can solve, such as:

Kelly had 8 blocks. Her friend gave her 5 more blocks. How many blocks does Kelly have in all?

[Note--at this point children should be able to solve JRU problems with sums between 10 and 20. This problem is chosen to be an addition (JRU) problem as a lead in to the next problem. The question part of this problem is stated to be similar to the upcoming problem.]

The teacher repeats the problem 2-3 times, while the children work on solving the problem. When the children have finished, the teacher invites a few students with different solution strategies to share how they solved the problem.

Then the teacher asks a problem of the new type:

Sam has 4 blue blocks and 2 yellow blocks. How many blocks does Sam have in all?

[This is a PPW-WU problem; it has items of the same type, but different colors, and they are items that one child has--I think that's a little easier than asking about items that two different children have. The problem is short, and it has smaller numbers than the last problem. The problem has gotten harder in terms of problem type, but it's quite easy in every other way]

The teacher repeats the problem, and waits while children work on the problem. It is expected that most children will create a set of 4 counters and a set of 2 counters. The teacher asks--"who can tell me what 'in all' means?" Children explain in their own words what "in all means". The teacher asks (to clarify) "does in all mean just the blue blocks?" (no) "does it mean just the yellow blocks?" (no). Who can show us how to count all of the blocks? The teacher calls on a child to show how to get the answer. Hopefully the child finds the answer of 6 blocks (and not the answer of 4 blue blocks and 2 yellow blocks). If the child does not answer correctly, the teacher gestures to the counters and repeats that s/he wants to know how many if you put them all together, and invites the child to push the counters together and count them again. After getting the answer "6 blocks" the teacher restates that "in all" means that it's how many in the group when you put them all one big group together.

The teacher follows up with a similar problem:

Brandon has 5 red buttons and 2 blue buttons. How many buttons does he have in all?

The teacher repeats the problem and waits while children work on the problem. S/he invites 2-3 children to share how they solved the problem. This is the end of the lesson.

This lesson uses the 3 principles I started out with:

It is moving from a simpler problem type to a problem type that is just one step more difficult than problems children have gotten good at solving, so it's moving slowly from easier to harder. A more typical lesson would have problems of the same problem type, but with gradually larger numbers (more typical because you don't introduce a new problem type every day).

It's building on childrens experience with JRU problems, it is asking problems using numbers children are confident with, and it is asking the problem in a context that is familiar to the children (assuming that they have colored building blocks in the classroom. If the classroom has does not have colored building blocks, another context should be chosen that is more familiar).

It's emphasizing the sense of the problem in several ways: having children share how they made sense of the problem, having children explain what the vocabulary means in the new context, and the teacher showing and summarizing what the problem means.

The lesson is doing one more key thing that isn't particularly unique to this type of lesson, and that is, the new problem which is solved and discussed is followed up by a very similar problem that can be solved in the same way. That immediate repetition is important for making the new ideas more solid.