Using derived fact strategies comes after learning counting strategies to solve addition and subtraction problems. A derived fact strategy means that there are some number combinations that the child knows and has memorized, and he or she uses those combinations to figure out (derive) other number combinations.
Children often memorize double facts fairly early on, so learning how to use doubles to figure out near-double facts is one of the first derived fact strategies children are able to use.
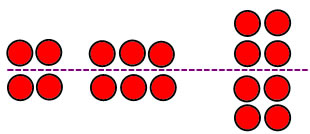
Before children can use doubles to solve other problems, they must first learn some of the doubles. Building pictures for doubles by using symmetry is one way for children to learn doubles, especially for doubles of numbers to 5. For example, children can place counters on either side of a symmetry line to show the double facts:

The standard dot cards suggested in the previous lesson also have dots grouped to show doubles:

As suggested in the Teaching Student-Centered Mathematics text, you can also make pictures or flash cards with common objects that show doubles. Unfortunately, it's rather hard to find good examples for some of the larger doubles:

Following the philosophy that children should always have a thinking strategy for figuring things out before they undertake practice and memorization tasks, it's worth noting a couple of thinking strategies for figuring out the larger doubles (doubles above 5+5).
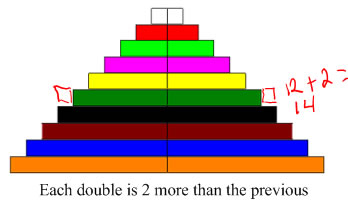
One strategy is well illustrated by a double Cuisenaire rod staircase. It shows how each double is 2 more than the last double, so if you know 6+6=12, then you can figure out 7+7=12+2=14
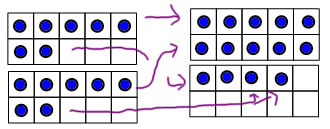
Another strategy is a 10-frame strategy that is sometimes called the "two 5's" strategy: if you can visualize 7 as 5+2, then you can see that the two rows of 5 make 10, and the two 2's make 4 more so 7+7=14:
Of course, once children have good ways of figuring out double facts, then it's time to practice so that at least some of them are memorized. Practice can be just flash cards, or it can be in the form of songs or rhymes or games. A lot of games can be modified to practice double facts--just provide one 10-sided die, and make the rule that you double the number on the die and go forward that many spaces, or collect that many points or tokens.
An introductory lesson using a word problem... Let's think about a class where the children have talked about and practiced doubles a little bit each day for several days (perhaps 2-3 weeks) and all of the children know at least some of the double facts. The teacher wants to introduce the idea of using double facts to solve facts that are near doubles. She might ask the class to think about the problem:
Sarah has 6 red balloons and 7 blue balloons. How many balloons does Sarah have?
After waiting for children to think and figure out a solution, she asks: who would like to share how they solved this problem?
Let's look behind the scenes: what did the teacher do when she prepared the question? First, she chose a PPW-WU problem--she wants to start out with a problem that doesn't have a change over time, because JRU change over time problems suggest counting on quite strongly, and she is hoping children will use the doubles they have been practicing instead of counting on. Second she chose numbers that are large enough that counting on isn't necessarily the obvious thing to do, and she chose numbers that are only one away from the double 6+6. The double of 6 is usually learned before the doubles of 7, 8 and 9, so she's giving a problem that is close to a double most children will know confidently. Now, she is hoping that some children will have used a double fact to figure out the problem.
Lets look at the scenarios that might play out next:
What if... Children solved the problem in several different ways. Someone volunteers a counting on strategy, someone else describes using 6+6 and adding one more, and yet another child describes using 7+7 and taking one away.
This is just what the teacher is hoping for. After listening to several strategies, she reminds the children of the two strategies that used doubles. She describes those strategies again, and then invites the children to try solving the next problem by thinking about a double that can help them. She then poses a similar problem:
Michael has 8 crayons.
Kyle has 7 more crayons than Michael.
How many crayons does Kyle have?
She has changed the problem type to another addition problem type, now that she is specifically asking children to think about doubles, and she has changed the numbers, but they are still just one more (or one less) than a double.
After children have had a few minutes to think, she follows up with some double questions:
And there you have a sample introductory mini-lesson for introducing the strategy of using doubles to add. Lets think for a minute about what variations there might be on a lesson like this:
What if... No one volunteered a strategy that used doubles? What could the teacher do then...
She could use questions to help children think about using doubles:
She could model the thinking she wants children to do:
In both cases she would follow up with another problem. Probably she would want to make the follow up question more similar to the first problem she gave because she would have lesson indication that the children were really ready and confident. She might choose a problem like:
Mandy has 5 Silly Bandz. Cheryl has 6 Silly Bandz. How many Silly Bands do they have all together?
Again, she would follow up with the same sorts of questions that are focused on using doubles:
Lesson variations:
Besides math talks about word problems with addends that are near doubles, some other good lessons and discussions are:
As a teacher, you are selecting appropriate problems for children to solve--ones that are appropriate and challenging for their knowledge, but not so difficult that they have to revert to more concrete modeling solutions. When children are learning how to use doubles to figure out other problems, they need to spend time at first working just with problems where using doubles is an appropriate and efficient thing to do.
Doubles +1 or -1: The easiest problems to apply knowledge of doubles to are the problems that are just one away from being doubles: doubles +1 and doubles -1:
| 3+4 4+5 5+6 6+7 7+8 8+9 |
4+3 5+4 6+5 7+6 8+7 9+8 |
It isn't that the ones on the left are doubles +1 and the ones on the right are doubles -1, its that children will choose to use a doubles +1 or -1 strategy depending on what doubles they know best. So, for instance, 7+8 can be solved from 7+7 with a doubles +1 strategy, and can be solved from 8+8 with a doubles -1 strategy. So, depending on whether the child recognizes and knows 7+7 or 8+8 with more confidence, they can apply a doubles +1 or a doubles -1 strategy to the problem.
Problems can be solved by a doubles +1 or a doubles -1 strategy if the two addends are only one apart.
Using a doubles +1 or a doubles +1 strategy requires 3 steps:
Doubles +2 or -2: The next set of problems that children can solve using doubles, are the ones that can be solved with a doubles +2, a doubles -2 or a sandwich doubles strategy. Problems can be solved by a doubles +2 or a doubles -2 strategy if the difference between the addends is 2 (one of them is 2 more or 2 less than the other).
3+5 |
5+3 6+4 7+5 8+6 9+7 |
There are three strategies that can be used to solve these problems. I'll use 8+6 as an example:
Doubles +2: If I know 6+6=12, and I see that 8 is 2 more than 6, then I can solve 8+6 by adding 12+2=14.
Doubles -2: If I know 8+8=16 and I see that 6 is 2 less than 8, then I can solve 8+6 by subtracting 16-2=14
Using a doubles +2 or a doubles +2 strategy requires 3 steps:
Sandwich doubles: If I realize that 6 is one less than 7, and 8 is one more than 7 (7 is sandwiched in between the other two numbers), then I can give one from the 8 to the 6 to get 8+6=7+7=14. 10-frames are good to illustrate this strategy:
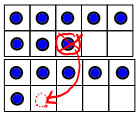
This strategy is a bit more sophisticated than the other two, and it doesn't have a standardized name (doubles +2 and doubles -2 are the names that everyone uses; sandwich doubles is a name I made up or I read somewhere or something), but it's fairly common as a strategy for children to invent. All of these strategies are ones where children are the best inventors, and the teacher's main job is to ask good questions.
Using the sandwich doubles strategy requires 3 steps:
Word problem types: Use doubles strategies rely on comparing the sizes of the two addends, so it's best to start with a static problem type when introducing problems that use doubles: PPW-WU is a particularly good one for this. After children have some experience with using doubles to solve problems, the teacher should be varying the problem types to include the other main addition problem types: CQU (with a more...than structure) and JRU.
Efficiency: Problems where the addends have a difference of 1 or 2 are generally considered to be problems where using doubles is an efficient strategy to use. When children are practicing the use doubles strategy, they should spend some time practicing just problmes where using doubles is an efficient strategy.
Timed tests: to work on speed while practicing a particular strategy (like using doubles) it's a good idea to make shorter tests that work on just the problems relevant for this strategy. These tests might have the same problems repeated several times on the same page--just in a different order. Rathmell's essays on basic facts drills have some good ideas for this.