Basic facts lesson:

Laying the foundations: Fluency with small numbers (Subitizing, Composing and Decomposing)

Who, What When Where Why:

Students in Kindergarten and first grade need to gain fluency with small numbers as a foundation for learning about larger numbers. Fluency means being able to visualize, combine and decompose small numbers. Small numbers are usually split into numbers up to 5, and then numbers up to 10.

Visualizing and Subitizing:

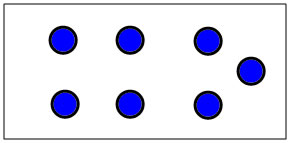
Subitizing means that you can recognize how many are in a set without counting. Being able to recognize and estimate small amounts increases childrens ability to think about numbers flexibly. Almost everyone can subitize amounts up to 3--it's easy to see without counting how many 1, 2, or 3 are. Above 3, we rely on patterns we are familiar with to recognize amounts. You can probably easily recognize 4, 5, and 6 dots if they are arranged in the pattern you find on dice, but you'd have more trouble if it were just 4, 5, or 6 dots in a line. There are several ways to organize dots or amounts so that they can be readily recognized without counting. Some valuable skills are:

• Recognize dots on a die without counting
• Be able to hold up a given number of fingers without counting (if the teacher says--hold up 7 fingers, children should be able to put up 7 fingers without counting them)
• Recognize dots on a 10-frame in standard positions without counting

Decomposing:

Decomposing a number means seeing it as made up of smaller parts, so when you think of 4 as 2+2, you are decomposing 4.

Visualizing and decomposing:

You can extend the dice dot patterns up to 10 in several ways. Think about this version for 7, 8, 9, 10:

These arrangements of dots are easily visulized and subitized because you can chunk them into easily recognized pieces. The dots and the are grouped into doubles and near doubles:7=4+3; 8=4+4; 9=5+4 and 10=5+5. These are the near double/near half decompositions, and they are very helpful for children to know, and ther're also the ones that are hardest to get to from counting up and back.

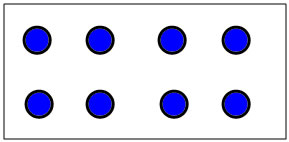
You can also visualize numbers by putting dots on a 10-frame in a standard way..

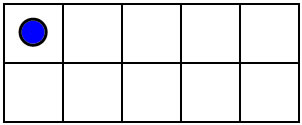
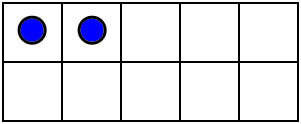
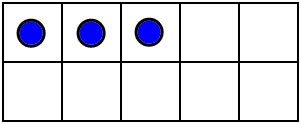
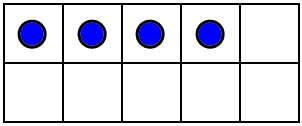
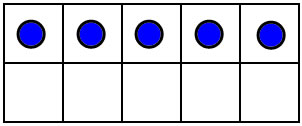
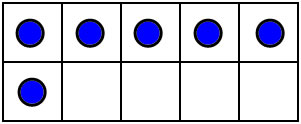
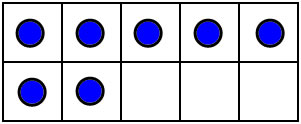
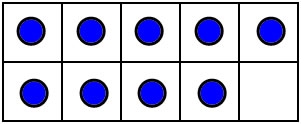
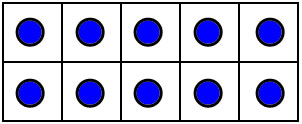
The 10-frame makes these dot patterns easy to visualize and subitize. 10 frame patterns and most finger combinations naturally compare numbers to 5 adn 10, and they teach the decompositions into 5 and some more: 6=5+1, 7=5+2, 8=5+3, 9=5+4, 10=5+5

These near doubles, comparing to 5, and knowing how many is 1 or 2 less or more cover almost all of the combinations that stay strictly below 10.

Number sense with dot patterns

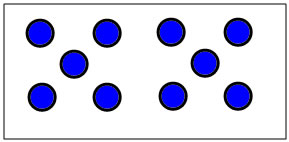
When teaching a standard set of dot patterns, such as those above, its helpful for the children to make the patterns with materials and by putting sticky dots on index cards. The most important thing, though, is to ask lots of questions. For instance, for the dot pattern for 9 you could ask:

What do you have to add to 5 to get 9? 4 and what makes 9? 4 and 5 more is the same as what number? If we take away the pattern of 5, what is left? If I have a pattern of 5, and you have the pattern of 9 how many more do you have than me? [2]

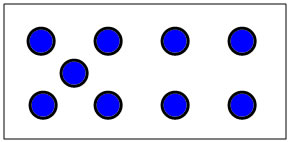
It's also useful to discuss other dot patterns with children. For instance, this set of dot patterns for 8 will probably ellicit several decompositions including 5+3 and 4+4

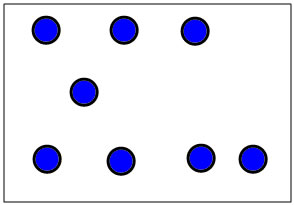
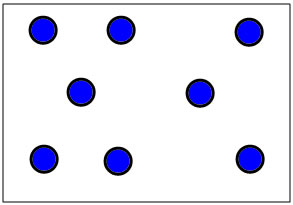
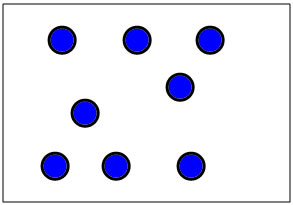
With new (non-standard) dot patterns the most important questions to ask are:

• How many dots do you see?
• How do you see them? [1]

Showing parts and wholes with Cuisenaire rods

Cuisenaire rods (like the set in your math kit) are useful for showing number relationships. Each color is a specific length, and the fact that the rods are not marked off into ones encourages seeing numbers as a quantity to be compared rather than as a discrete set to be counted. Cuisenaire rods are more abstract than dots and 10-frames, so they are primarily a first and second grade material rather than a kindergarten material. It takes a while for children to become comfortable with the number-size-color correspondence, so it's appropriate to begin working with Cuisenaire rods with several activities that are exploratory. Once children become comfortable with the material it can be useful in several ways:

• Show a random number of white cubes from the set (10 or less), and ask children to estimate how many there are. Then let children line them up and compare to the longer rods to find out how many. Estimation of values within 10 is helpful for having a sense of when answers are reasonable in number work.
• Have children write down pairs that make the same length as a given rod. For example, children could copy this relationship onto grid paper, and write the number sentence 5+2=7 that goes with it.

• Make a Cuisenaire rod staircase showing all of the decompositions of a number

8=8+0 8=7+1 8=6+2 8=5+3 8=4+4 8=3+5 8=2+6 8=1+7 8=0+8 Note--it's a good idea to vary the way you write equations--sometimes write equations the usual way: 5+3=8 and 8-3=5, but children get a better understanding of equations if you vary this with 8=5+3 and 5=8-3.

Practice Makes Perfect

Number sense and fluency builds slowly, so it's important to build it steadily. Number Talks, where you show a dot pattern or pose a short problem and then invite children to share their strategies, are one good way to revisit number ideas regularly with students. You can also find and make games for children to play to practice composing and decomposing small numbers.

You can make both solitaire and competitive games for decomposing a single number with deck of number cards that are smaller than the number to be decomposed. For example, to practice decomposing 6, you would need to make a set of 4 cards each of the numbers 1-5. To start play, you lay out a given number of cards (4 for a competitive game, 5 for a solitaire game), and the players take pairs of cards that add up to 6, replacing the used cards at the end of the turn. In the solitaire game, the goal is to clear the deck and pair up all of the cards. In the competitive game, the goal is to collect the most pairs--if no pair can be made, the player turns over another card and play passes to the next player.

The game Shut the Box is a dice game that practices decomposing numbers to 12, where the number to be decomposed is the sum of two rolled dice.

Summary

The two important things for children to learn about numbers below 10 that we've discussed here are:

• Subitizing numbers in at least one visual pattern (dots, 10-frame or fingers). Subitizing means recognizing the number (and being able to build the number) without counting.
• Decomposing numbers into number partners whose sum is that number.
  • Referring to a visualized pattern that they can subitize is helpful for decomposing numbers.
  • Talking about numbers and visualized number patterns are helpful for decomposing numbers (math talks).
  • Playing games that practice number decompositions is helpful for decomposing numbers.
  • Asking the same question in lots of different ways about a number, and writing the number sentences in lots of different ways helps children understand all of the related meanings that a decomposition has.

References: Most of the material in this lecture is taken from the books:

[1] Number Talks: Helping Children Build Mental Math and Computation Strategies by Sherry Parrish

[2] The Dyscalculia Toolkit by Ronit Bird