Basic Facts Lesson 2.11: Back down through ten to subtract

Back down through ten to subtract is another useful strategy for subtracting from numbers between 10 and 20.

Back down through ten can be described as a take-away strategy: the goal is to take away the subtrahend from the minuend and see what is left.  While this works just fine in a part-whole model, the part whole model isn't needed--take away (SRU) thinking works just fine. It is also a bridge through 10 strategy: we take away enough to reach 10 and then take away the rest, so 10 is our benchmark and stepping stone along the way.

15-6

We can represent the thinking in backing down through 10 using several different materials:

With 10-frames, we begin with the minuend (15) and proceed to take away 6 by first taking away all of the counters on the right 10-frame, and then taking away one more counter on the left 10 frame (the answer is the remaining number of counters)

On the open number line, you can see that what we are doing is starting with the minuend (15) and taking away enough to get down to 10.  Then we compare that to the subtrahend and figure out how many more we need to take away/count down so that we have taken away a total of 6.

Numerically, we break the subtrahend (6) down into the amount in the ones digit of the minuend (5) and some more (1), so 6 is made of the parts 5 and 1.  If we take away first 5 from 15, we get 10, and then the remaining amount (1) from 10, we get 9.  Notice that the steps of subtracting to reach 10, and subtracting the rest from 10 get their own separate number sentences.

The Cuisenaire rod process is a lot like the number process.  We first break down 6 into 1 and 5, and then we break 10 into 9 and 1, so that we see that the missing part is 9.

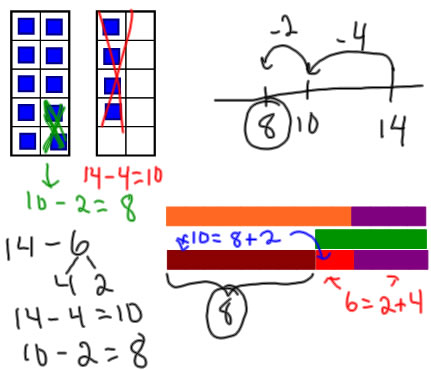
14 - 6 is another problem that backing down through 10 is a good strategy for.

Removing the 4 counters from the right 10-frame leaves 10, and removing 2 more counters (6 total) leaves 10-2=8.

Subtracting 4 from 14 on the number line takes us to 10. We still need to take away 6-4 =2  more, so that gets to the answer of 8.

Numerically, we need to know that 6 can be decomposed into 4+2.  After taking 14-4=10, we still need to take away 2 more, and 10-2=8.

With the Cuisenaire rods, we line up to show that 6=2+4 and that 10=8+2.  Thus, 14 splits into sets of 6 and 8: 14-6=8.
There are facts, like 12-9, for which backing down through 10 can be used, but it's harder to visualize, and not as efficient. What makes it more difficult (and hence less efficient) is that when you subtract down to 10, there's still a lot of subtracting to do: 12-2=10, but having taken away 2 isn't very close to having taken away all of 9.

Prerequisite knowledge:

Children mostly need practice composing, decomposing and visualizing numbers  The specific compositions and decompositions needed are:

With this strategy, and some practice, children can solve some of the subtraction facts where the minuend is greater than 10 (and the difference is less than 10).  All of the subtraction facts where the minuend is greater than 10 and the subtrahend and difference are less than 10 can be solved by either building up through 10 or backing down through 10, but some facts are easier to solve this way than others are.

Facts where it's efficient to solve by backing down through 10 (those facts where taking away the 1's digit of the minuend is nearly as much as taking away the subtrahend) Facts that can be solved by backing down through 10, but it's not efficient. (those facts where there's comparitively more left to be subtracted after taking away the 1's digit of the minuend).
18 - 9
17 - 8
16 - 7
15 - 6
14 - 5
13 - 4
12 - 3
11 - 2

17 - 9
16 - 8
15 - 7
14 - 6
13 - 5
12 - 4
11 - 3

15 - 9
14 - 8
13 - 7
12 - 6
11 - 5

14 - 9
13 - 8
12 - 7
11 - 6

12 - 9
11 - 8

13 - 9
12 - 8
11 - 7

 

11 - 9

Notice that in the facts where it is efficient, the minuend is just 1 or 2 more than the ones digit of the subtrahend.