7=5+2
10=9+1Using derived fact strategies comes after learning counting strategies to solve addition and subtraction problems. A derived fact strategy means that there are some number combinations that the child knows and has memorized, and he or she uses those combinations to figure out (derive) other number combinations.
This section looks at facts children can figure out if they know some particular facts:
Children learn how to decompose and compose numbers less than 10 by experience with adding, subtracting, counting and exercises for subitizing numbers by recognizing patterns. For example, dot patterns and 10-frames can help children learn decomposing numbers.
7=5+2 |
10=9+1 |
Practice with Cuisenaire rods, 10 frames and dot patterns can all be used to teach doubles facts:
A double Cuisenaire rod staircase shows the doubles of 1-10 |
Doubles on ten frames or a Rekenrek bead frame can help children see patterns like two sevens is made of two fives (which makes 10) and two 2's, so 7+7=10+4=14 |
Learning to add 10 to make teen numbers is reinforced when you use materials that show teen numbers as 10 and some more.
The strategy of using doubles means that children use a doubles fact that they know to figure out another fact that is close to being a double. Some particular sub-categories of using doubles are:
Doubles +1/-1
The problem 6+7 can be solved using a doubles +1 or a doubles -1 strategy.
A child who knows how to double 6 might notice that 7 is one more than 6, so 6+7 can be solved by doubling 6 and then adding 1.
A child who knows the double of 7 might notice that 6 is one less than 7, so 6+7 can be solved by doubling 7 and then subtracting 1.
A doubles +1 or -1 strategy can be used with this problem because one addend is one greater than the other: the addends are 1 apart.
Doubles +2/-2 and Sandwich doubles:
The problem 8+6 can be solved using the strategies doubles +2, doubles -2 or a strategy I'm calling sandwich doubles.
A child who knows the double of 6 might notice that 8 is 2 more than 6, so to find 8+6, you can double 6 and add 2 (doubles +2 strategy)
A child who knows the double of 8 might notice that 6 is 2 less than 8, so to find 8+6, you can double 8 and subtract 2 (doubles -2 strategy)
A child who knows the double of 7 might notice that if you give one from the 8 to the 6, you get two 7's, so to the sum of 8+6 is the same as the double of 7 (this is what I'm calling sandwich doubles--7 is sandwiched between 6 and 8)
The strategies doubles +2 and -2 and sandwich doubles work for problems where one of the addends is 2 more than the other (the addends are 2 apart).
Efficiency:
Using doubles is an efficient strategy if the two addends are close together--only 1 or 2 apart. These are exactly the problems that can be solved by the sub-strategies doubles +1/-1 and doubles +2/-2.
What is important for introducing using doubles?
CGI type of the problem is not very important for introducing using doubles. It might be better to start with a PPW-WU than a JRU problem (because JRU is associated with counting on), but the numbers in the problem are more important than the word problem type for children learning how to use derived fact strategies.
It is important that you choose numbers where using doubles is an efficient and natural strategy: starting with addends that are 1 apart, and later asking questions where the addends are 2 apart.
The make 10 strategy is also called the bridge through 10 strategy. It can be used whenever both addends are less than 10 and the sum is more than 10, though it's easiest to use if one of the addends is 8 or 9.
To use the make 10 strategy, the child recognizes that one of the addends is close to 10 (but a little less), and if you add on the other one, you will get more than 10. Then the child decomposes the other number so that they can turn the sum into 10 and some more.
Representations
It's a good idea to have some ways of representing the make 10 strategy. Manipulatives and diagrams to clarify the make 10 strategy are a very good idea. Here are some ways to show the make 10 strategy with some appropriate materials.
With 10-frames
For example, to figure out 8+5, we realize that 8+2=10
Then we partition 5 into 2+3, and take 2 from the 5 and give it to the 8 to make 10. This leaves us with 10+3:
So the sum is 13.
Rekenrek
You can show the same thing on a 2-bar Rekenrek by sliding beads back and forth:
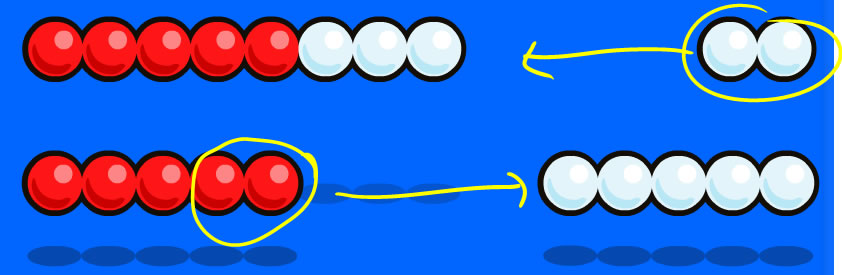... becomes...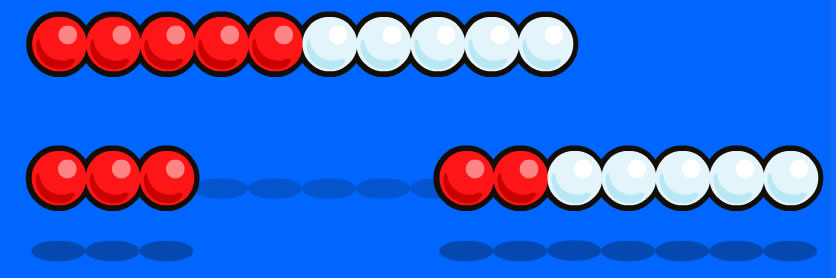 
An open number line is a very good way of showing the make 10 strategy for adding:
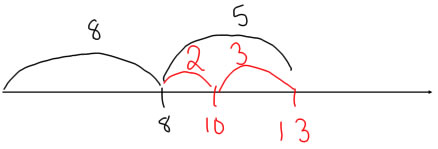
Being an open number line means that instead of writing onto the number line all of the numbers before you start, you write on just the ones you need in order to keep track of what you are doing. This number line diagram shows 8+5, and of course, the jump to 8 lands at 8, but it's not obvious where the jump of 5 will land. To figure that out, you have to break 5 into 2+3. The jump of 2 lands you right on 10, and jumping 3 from 10 lands you at the sum of 13.
With the open number line, you should start with the larger addend--the one that is closest to 10--because that's what you want to add on to in order to make 10
Make 10 works with higher numbers: It works well to practice the make 10 strategy with sums where one addend is a single digit, and the other is a two-digit number is just less than a multiple of 10
Efficiency
Make 10 is considered a fast efficient strategy when the sum is more than 10 and one of the addends is 8 or 9. It isn't considered efficient for other sums largely because of the need to decompose the second number. Decomposing any number into 1 or 2 and some more is easier than the other decompositions, and if, for example, you wanted to use the make 10 strategy for 7+5, you would be using 7+3=10, so you would need to decompose 5 into 3 and some more, which is harder to visualize than decomposing 5 into 2 and some more (even though it's exactly the same decomposition). Make 10 can be used for any problem where the sum is more than 10, though it may not be considered efficient.
It isn't considered efficient for other sums largely because of the need to decompose the second number. Decomposing any number into 1 or 2 and some more is easier than the other decompositions.. Make 10 can be used for any problem where the sum is more than 10 and the two addends are less than 10, though it may not be considered efficient.
What's important?
CGI type isn't particularly important for this strategy (or for any of the derived facts strategies). JRU is an appropriate problem type to use at the beginning because make 10 uses an adding on to higher way of thinking which is close to the counting on from higher counting strategy.
Manipulatives that show groupings by 10 are particularly useful for introducing and thinking about make 10 strategies. Ten frames and Rekenreks are examples of manipulatives that group by tens. You can also show how 10 is an important number with an open number line representation.
When introducing make 10 it's helpful to start with numbers that the strategy would be particularly good for. It's easiest to figure out a make 10 strategy if the first addend is 9 (only one less than 10), and the other addend is not too small (not 1, 2 or 3). Later children should practice with sums that have 8 and 9 as one of the addends, and where in some problems the larger addend is first, and in some problems the larger addend is second..
Make 10 is a particularly powerful thinking strategy because our number system is grouped by tens, so looking for tens is a really useful way to look at numbers.
