3 digit addition

Base 10 Lesson 3.4: Extending place value: 3 digit addition

Two digit addition is a focus of second grade, three digit addition is a focus of third grade. It's often beneficial to revisit addition using base 10 blocks again in third grade to reinforce the place value understandings necessary for 3 digit addition with regrouping.

The upcoming video assignment is to practice the teaching step of making connections between solving with base 10 blocks and the standard algorithm.

In my examples, I am using a place value mat. A place value mat organizes the manipulatives by place value. A place value mat is organized so that the place values of the manipulatives are in the same order they are written with numbers : 1000's on the left and 1's on the right. While you don't have to use a place value mat for your example, you should arrange your materials so that the 1's are on the right, and the 100's are on the left so that it matches the order in which we write numbers.

Working with base 10 blocks and similar materials is helpful for understanding addition and subtraction, but in order for that understanding to carry over to using a standard algorithm, we have to carefully build the connections between the manipulative work and the standard algorithm. One part of building those connections is being able to explain it as the teacher. I am looking for some specific things for you to include in your teacher-explanation:

You should be able to explain in an order where you start with what you do with the manipulatives, and then explain how to write it down with numbers (even though the standard algorithm is very concrete for you because you have done it many times, it will not be concrete for the children who are just learning it--for them the manipulatives are more concrete). Pretend that you are explaining to a child who is secure with solving using manipulatives, but who does not yet know the standard algorithm.
You should explain each "carry" in terms of what the number represents and where it comes from in the manipulative work. I don't like the word carry, because we are all in the habit of saying things like "carry the 1", which is shorthand for "write 1 in the tens/hundreds place to show the 1 ten/ 1 hundred we got from making a trade in the ones/tens place". It's not so much the word "carry" that's a problem, it's that when you use the word carry, you're not explaining the meaning. As a teacher you need to be able to explain meaning, and that's something I want you to show in this assignment. I recommend the words: trade or exchange (synonyms) and write or record (synonyms) to describe what you are doing because it will help you remember to explain the step.
You should use the descriptors: tens and hundreds as much as you can. When you are adding 5+6 in the tens place, what you should be saying out loud is 5 tens plus 6 tens or fifty plus sixty. .

Here are my examples:

	We're going to add 3 hundred and eighty four to two hundred and seventy nine.
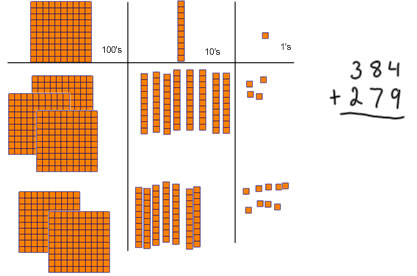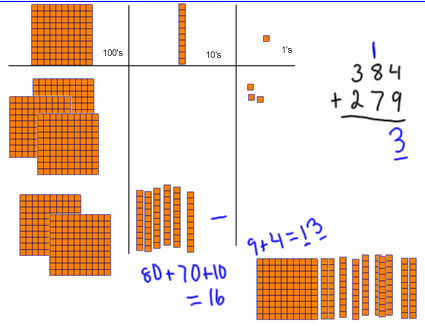
	The first thing we do with the manipulatives is to get out three hundreds, 8 tens and 4 ones, and then get out 2 hundreds, 7 tens and 9 ones. [notice that I am starting with the manipulatives]
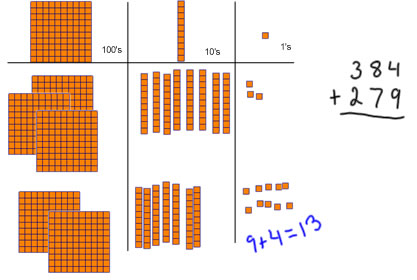	Now we look at the ones place: we have 4 ones and 9 ones, and we put them together, and we get that 4+9=13 ones. I give one from the 4 to the 9 to make it 10, so we have 13=10+13.
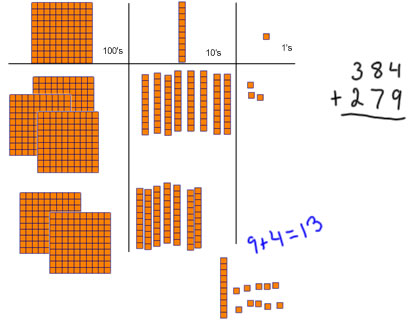	I trade in 10 ones for a ten, which is a fair trade because 10 ones = 1 ten. Next, I'll put the ten in the tens place on the place value mat. [notice that I am reinforcing that we trade 10 ones for a ten because those are equal values]
	I'm done with the ones, so I need to stop and write down what I did. I added 4+9 and got 13, which is 10 and 3. The 3 ones are going to be my final number of ones, so I write them in the answer. I traded 10 ones for a 10, and I need to show that tens stick in the number work, so I put a 1 over the tens place to show the ten that we got from 13. [notice that I explained the carry step by describing it as a ten, and as a tens stick, I also repeated that it came from the ten in 4+9=13. Notice that I did this after I did the manipulative work in the ones place, but before adding any tens]
	In the tens place we have 8 tens plus 7 tens plus 1 more ten that came from trading in the ten from 13. 8+7=15, and 1 more is 16, so 8 tens +7 tens + 1 ten = 16 tens. I move 2 tens up to the top row of tens so it's grouped as 10 tens and 6 tens. [notice that I am describing the addition as 8 tens plus 7 tens plus 1 more ten, not as 8+7+1]
	I trade 10 tens for 1 hundred block. That's a fair trade because 10 tens is equal to 100. [fair trade explanation]
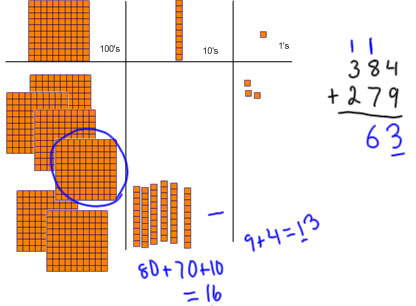	I have done everything with my tens, so I'm going to stop and record my work with numbers. I added 8 tens +7 tens + 1 ten = 16 tens, which is 1 hundred and 6 tens. The 6 tens is my final amount for the tens place, so I write 6 in the tens place of the answer. The 10 tens, I traded for a 100 block, and put it in the hundreds place, so I write 1 in the hundreds column to represent the 1 hundred block that I got from trading in 10 tens from 16 tens. [explain where that trade comes from]
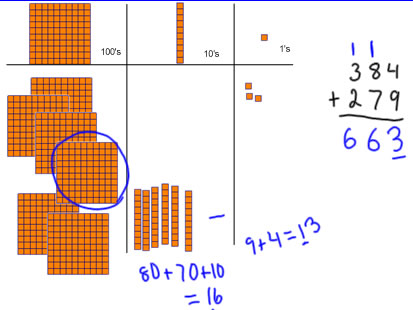	Add the hundreds: 3 hundred plus 2 hundred plus 1 more hundred is 6 hundreds. That's my final number of hundreds, so I write 6 in the hundreds place of my answer.

Example 2:

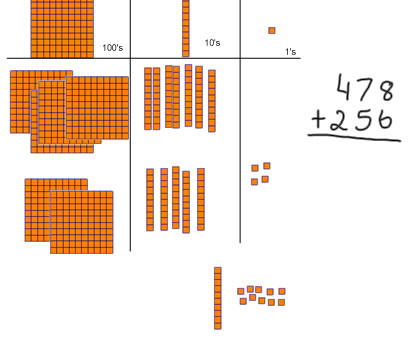
	We're going to add 478 to 256. The first thing we do is to take out base 10 blocks to show 478 and 256, (4 hundreds, 7 tens and 8 ones, 2 hundreds, 5 tens and 6 ones). Next we'll start on the right and combine the ones.
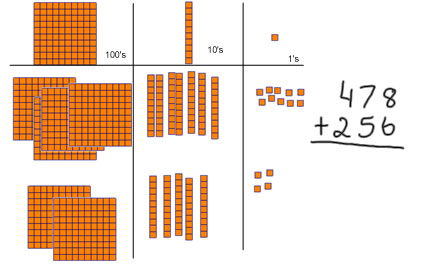	8+6=14. I moved 2 from the 6 up to the 8 to make 10. 14=10+4. When we have a group of 10, we trade that group of 10 ones for a 10 stick. That's a fair trade beacause 10 ones and a 10 stick are worth the same amount
	When we have a group of 10, we trade that group of 10 ones for a 10 stick. That's a fair trade beacause 10 ones and a 10 stick are worth the same amount
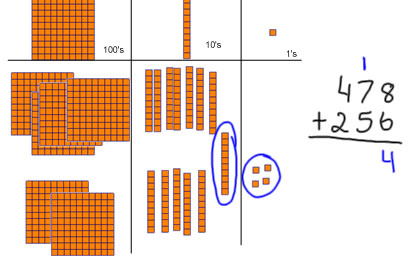	Now when I'm done with the ones, I stop and write that down with numbers. 8+6 = 14, that's 10+4. The 4 stayed in the ones place, and I write that in the ones place as my final amount of ones. I write a 1 up above the tens place (1 ten) to show the 10 from 10+4--that's the tens stick we traded for. I put it up above the tens because we're not done with the tens yet, so I want to leave the answer space for our final number of tens. Now we combine the tens: we have 7 tens plus 5 tens plus the 1 more ten we got from trading in 10 ones. 7+5=12 so 7 tens plus 5 tens = 12 tens or 120. Add one more ten to get 13 tens or 130.
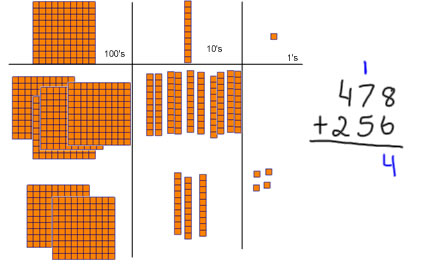	So I move the tens to make a group of 10 tens. 13 tens = 10 tens + 3 tens. 10 tens = 100, so 13 tens = 1 hundred + 3 tens.
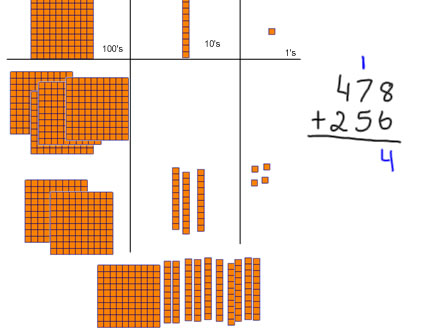	I take the 10 tens and trade it for a 100 block. It's a fair trade because 10 tens = 100. If you put those 10 tens together, it would be the same size as the 100 block.
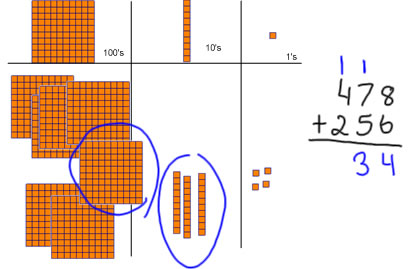	Now I'm done with the tens, and I need to stop and write down what I did. I added 7 tens +5 tens +1 ten = 13 tens, and 13 tens is 1 hundred and 3 tens, so I put 3 in the tens place of the answer (that's the final number of tens), and I write a 1 above the hundreds place to show the 1 hundred that came from 13 tens.
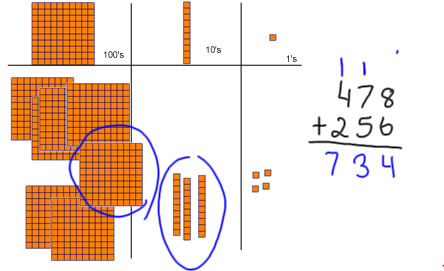	The last thing to do is to add up the hundreds. I have 4 hundred plus 2 hundred plus 1 more hundred (that we got from trading 10 tens), and that makes 7 hundred. I write 7 down in the hundreds place, and there isn't any more trading I need to do because 7 is less than 10.