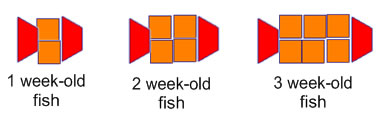
The following questions refer to the pattern block fish pattern:

1. Which of the following questions would be appropriate to ask of kindergarten children?
a. Make a 4 week-old fish using pattern blocks
b. Tell how many pattern blocks you need for a 1 week old fish, a 2 week old fish and a 3 week old fish.
c. Tell how many pattern blocks you need for a 4 week old fish
d. Tell how many pattern blocks you need for a 5 week old fish
e. Tell how many pattern blocks you need for an 8 week old fish
f. Tell how many pattern blocks you need for a 10 week old fish
g. Tell how many pattern blocks you need for a 20 week old fish
h. Tell how many pattern blocks you need for a 100 week old fish.
a-d can easily be solved by building the fish from pattern blocks, and so are appropriate for kindergarten and first graders.
2. Which of the above questions would be good for third graders?
d, e and f are good third grade problems because they can be reasonably found by looking at the numbers of tiles in the first 4 fish and skip counting. g and h are good to do with third graders in a group to expose them to looking for multiplication rules, but are really more clearly grade 5-6 problems.
3. Make a table showing the age of the fish and the total number of pattern blocks you need to make it. How does this table help you answer the questions in #5? What sort of reasoning does this table encourage?
| age (in weeks) | total number of pattern blocks |
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
| 4 | 10 |
You can see that the total number of blocks goes up by 2 every time. This table makes it easy to skip count to find the answers to #5.
4. Make a table showing the age of the fish, the number of pattern blocks of each type, and the total number of pattern blocks. How does the table help you answer the questions in #5? What sort of reasoning could you have from this table that would be different from the reasoning in #7?
| age (in weeks) | number of squares | number of trapezoids | total number of pattern blocks |
| 1 | 2 | 2 | 4 |
| 2 | 4 | 2 | 6 |
| 3 | 6 | 2 | 8 |
| 4 | 8 | 2 | 10 |
This table helps you see that the number of squares is double the age and there are always 2 trapezoids, so the number of squares is double the age plus 2.
5. Why do we call this kind of pattern a growing pattern rather than a repeating pattern?
We call it a growing pattern because we are focusing on the total number of pattern blocks, and that amount grows as the pattern goes along.
6. How can you use multiplication to find out how many pattern blocks are in an N week old fish?
2×N+2