1. This fractal rule for the fractal Cantor dust is: take
out the middle third or each segment in the previous iteration.
A. Draw the next iteration of the fractal
| iteration 0 |
 |
| iteration 1 |
 |
| iteration 2 |
 |
| new: iteration 3 |
 |
B. Complete the table below, and explain your rule for finding the numbers
that go in the table
| iteration number |
number of pieces |
length of each piece |
total length |
| 1 |
1 |
1 |
1 |
| 2 |
2 |
1/3 |
2/3 |
| 3 |
4 |
1/9 |
4/9 |
| 4 |
8 |
1/27 |
8/27 |
| ... |
this doubles each time because a single segment it traded for two smaller
segments. |
the denominator is multiplied by 3 each time OR the length is multiplied
by 1/3 each time because when you remove the middle third, the segments
left are each 1/3 as long as the previous segment |
... |
2. The fractal rule for the Koch curve is to replace each
segment with a new shape (shown below) which is formed by erasing the middle
third, and putting in two segments that would make an equilateral triangle
in its place:
Segment was: |
Changed to: |
 |
 |
A. Draw the next iteration:
| iteration 0 |
 |
| iteration 1 |
 |
| iteration 2 |
 |
| new: iteration 3 |
 |
B. Complete the table below, and explain your rule for finding the numbers
that go in the table
| iteration number |
number of pieces |
length of each piece |
total length |
| 0 |
1 |
1 |
1 |
| 1 |
4 |
1/3 |
4/3 |
| 2 |
16 |
1/9 |
16/9 |
| 3 |
64 |
1/27 |
64/27 |
| |
multiply be 4 because each segment is replaced by 4 smaller segments* |
divide by 3 (or x 1/3) because when you remove a middle third the remaining
segments are 1/3 as long as the previous one** |
|
* Each segment replaced by 4 smaller segments:



**New segments are 1/3 as long as previous segments



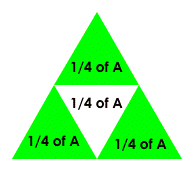
2. The fractal rule for the Sierpinski triangle is to replace
each (point up) triangle with a new shape (shown below) which is formed by
connecting the midpoints of its sides, and erasing the middle, leaving 3 smaller
triangles:
triangle was |
Changed to: |
 |
 |
A. Draw the next iteration:
| iteration 0 |
 |
| iteration 1 |
 |
| iteration 2 |
 |
| new: iteration 3 |
 |
B. Complete the table below, and explain your rule for finding the numbers
that go in the table
| iteration number |
number of sements |
length of each segment |
total length |
| 0 |
3 |
1 |
3 |
| 1 |
9 |
1/2 |
9/2 |
| 2 |
27 |
1/4 |
27/4 |
| 3 |
81 |
1/8 |
81/8 |
| |
multiply previous number by 3 because you are getting 3 times as many
triangles every time (and each triangle has 3 sides)* |
divide by 2 (or x1/2) because the side length of a smaller triangle
is half as long as the larger triangle it came from |
|
* 3 times as many triangles every time (and each triangle has 3 sides)
 |
 |
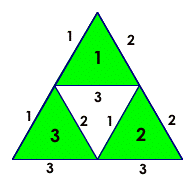 |
| 1 triangle (x3 sides) |
|
1x3 triangles (x3 sides) |
C. Complete the table below, and explain your rule for finding the numbers
that go in the table
| iteration number |
number of triangles |
area of each triangle |
total area |
| 0 |
1 |
1 |
1 |
| 1 |
3 |
1/4 |
3/4 |
| 2 |
9 |
1/16 |
9/16 |
| 3 |
27 |
1/64 |
27/64 |
| |
multiply by 3 because each triangle is replaced by 3 smaller ones* |
divide by 4 (or x 1/4) because each triangle is 1/4 as big as the one
it came from** |
|
*each triangle is replaced by 3 smaller ones


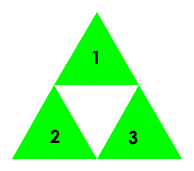
*each triangle is 1/4 as big as the one it came from

2. The fractal rule for the Sierpinski carpet is to replace
each square with a new shape (shown below) which is formed by cutting the
square into 9 smaller squares at the 1/3 points of the sides, and then removing
the center square:
square was |
Changed to: |
 |
 |
A. Draw the next iteration:
| iteration 0 |
 |
| iteration 1 |
 |
| new: iteration 2 |
 |
B. Complete the table below, and explain your rule for finding the numbers
that go in the table
| iteration number |
number of squares |
area of each square |
total area |
| 0 |
1 |
1 |
1 |
| 1 |
8 |
1/9 |
8/9 |
| 2 |
64 |
1/81 |
64/81 |
| 3 |
512 |
1/729 |
512/729 |
| |
multiply by 8 because each square is replaced by 8 smaller squares * |
divide by 9 (or x 1/9) because it takes 9 smaller squares to make a
larger square every time, so each is 1/9 as large as the previous ** |
|
*each square is replaced by 8 smaller squares


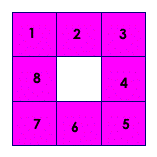
**each is 1/9 as large as the previous























