Untitled Document

We are studying self-similar fractals right now.

A shape is self similar if it is made out of several smaller copies of itself.
These self-similar fractals are made by performing a recursive rule on a shape. You start with a given shape, and then do the rule over and over to the shape. To get the perfect fractal, you have to imagine doing the rule infinitely many times.
Each new version you get after doing the rule is called an iteration.

On the next quiz, you will be asked to do the following thing for one or two fractals:

1. Draw out the next iteration, after you have been shown the first 2 or 3 iterations.

2. Make a table and figure out a formula for the length of a fractal.

3. Circle a part or parts that are similar to the whole (but are smaller than the whole)

Sample problems:

1. This fractal rule for the fractal Cantor dust is: take out the middle third or each segment in the previous iteration.

A. Draw the next iteration of the fractal

iteration 0
iteration 1
iteration 2

B. Complete the table below, and explain your rule for finding the numbers that go in the table

iteration number	number of pieces	length of each piece	total length
0	1	1 m.	1 m.
1
2
3

2. The fractal rule for the Koch curve is to replace each segment with a new shape (shown below) which is formed by erasing the middle third, and putting in two segments that would make an equilateral triangle in its place:

Segment was:	Changed to:

A. Draw the next iteration:

iteration 0
iteration 1
iteration 2

B. Complete the table below, and explain your rule for finding the numbers that go in the table

iteration number	number of pieces	length of each piece	total length
0	1	1	1
1
2
3

3. In this Koch curve, circle a piece that is the same shape as the whole curve.

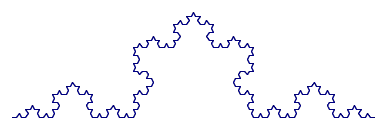
4. The fractal rule for the Sierpinski triangle is to replace each (point up) triangle with a new shape (shown below) which is formed by connecting the midpoints of its sides, and erasing the middle, leaving 3 smaller triangles:

triangle was	Changed to:

A. Draw the next iteration:

iteration 0
iteration 1
iteration 2

B. Complete the table below, and explain your rule for finding the numbers that go in the table

iteration number	number of sements	length of each segment	total length
0	3	1 m	3
1
2
3

C. Circle a piece that is the same shape (but smaller) as the whole shape.

Sierpinski triangle

Answers