#4: What is tricky about this is coordinating the vertices and edges of the triangle

Correct ways to split up the triangle	V, F and E for correct ways	Incorrect ways to split up the triangle	What's wrong
	V=3, E=3, F=2 3-3+2=2		Edges have to go between vertices, so there has to be at least one vertex.
	V=1, E=1, F=2 1-1+2=2		Edges go between vertices. If there isn't a vertex, the edge just keeps going--an edge doesn't split into two edges without a vertex.

5. Again, it's the tricky triangles that cause the problems

Correct ways to split up the shape	V, F and E for correct ways	Incorrect ways to split up the shape	What's wrong
	V=2, E=3, F=3 2-3+3=2		Edges go between vertices. If there isn't a vertex, the edge just keeps going--an edge doesn't split into two edges without a vertex.
	V=6, E=7, F=3 6-7+3=2

6. Surprise, surprise, it's tricky triangles that cause problems again (maybe I should have made up some problems with tricky squares)

Correct ways to split up the shape	V, F and E for correct ways	Incorrect ways to split up the shape	What's wrong
	V=2, E=3, F=3 2-3+3=2		Edges go between vertices. If there isn't a vertex, the edge just keeps going--an edge doesn't split into two edges without a vertex.
	V=4, E=5, F=3 4-5+3=2

Book problem #5;

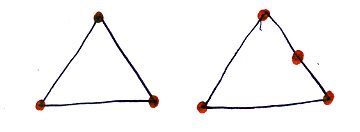
If you add another vertex, then you also add another side, so V goes up by 1, and E goes up by 1

Before:.............................After:

V=3, E=3, F=2................V=4, E=4, F=2

The Euler characteristic V-E+F goes up by 1 for V, and then down by 1 because of E, so it stays the same.

7. If you number the shapes from left to right a, b, c, d:

a. V stays the same, E goes up by 1, F goes up by 1, so V-E+F stays the same (-1+1=0 change)

b. V goes up by 1, E goes up by 1, F stays the same, so V-E+F stays the same (1-1=0 change)

c. V stays the same, E goes up by 1, F goes up by 1, so V-E+F stays the same (-1+1=0 change)

d. V goes up by 1, E goes up by 1, F stays the same, so V-E+F stays the same (1-1=0 change)