
2. More of the spiral:

The spiral is made by drawing quarter circles inside squares:
| Where the squares have Fibonacci number sizes: 1x1, 1x1, 2x2, 3x3, 5x5, etc. |  |
3. You can get the golden ratio by taking ratios of Fibonacci numbers. The bigger the Fibonacci numbers, the closer their ratio gets to being exactly the golden ratio (the golden ratio is often called the golden mean)
You get either .618 or 1.618 depending on whether you divide: small/big
| 1/1 | 1/2 | 2/3 | 3/5 | 5/8 | 8/13 | 13/21 | 21/34 | 34/55 | 55/89 |
| 1 | .5 | .667 | .6 | .625 | .615 | .619 | .617 | .618 | .618 |
or whether you divide: big/small
| 1/1 | 2/1 | 3/2 | 5/3 | 8/5 | 13/8 | 21/13 | 34/21 | 55/34 | 89/55 |
| 1 | 2 | 1.5 | 1.667 | 1.6 | 1.625 | 1.615 | 1.619 | 1.618 | 1.618 |
Note: The golden ratio is approximately either .618 or 1.618 (depending on who you ask) , and those numbers have the curious property that 1/.618=1.618 and 1/1.618=.618
(This isn't exactly true because .618 isn't exactly the golden ratio, it's just really close. The golden ratio is exactly
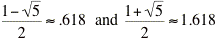
and sometimes we use the greek letter φ to represent it)