Fun Math Comic
I thought this was a funny comic from Calvin and Hobbes.

I thought this was a funny comic from Calvin and Hobbes.

While I was reading a post from a fellow blogger, one in particular caught my attention http://sweeneymath.blogspot.com/ . What to do when a student fails, or is failing? Not necessarily just a test or a class, but even when they fail to comprehend a topic or idea, as a teacher what are you supposed to do? As Mr. Sweeney explains his dilemma of not wanting to give students a failing grade, but also not wanting to give them a grade they didn’t earn, he also explains his concern that many kids now have never failed anything before. I’ve personally read stories about how schools have had to add more sports teams because they have more students wanting to play than they have room for, and trying out to be on a sports team didn’t fly with the parents. They weren’t about to let their child miss out on an opportunity, and with enough complaints to the right people, schools were forced to let the students play. (Sorry I don’t have a source for this, I just remember reading about it) I’m sure that we could all think of several more examples where students, or even kids in general were given something, despite maybe not earning it, simply because it “wasn’t fair”. But what kind of a disservice are we giving these kids? If they go through life getting things just because other people do, they will, and do, come to expect it. Once they get into school, and these ideas continue, the idea of “failing” will be a shock of reality. Back to what Mr. Sweeney had to say, he required any student who fails a test, or to understand an idea, a retest. While I do think he has the right idea, and that students do need to go back and learn what they missed the first time around, is it fair to the students who did the work to understand it the first time around? Or should that not matter, as long as at the end of the day, every student has learned what they need to?
I was browsing around looking at other blogs on the web and came across The Math Less Traveled at http://www.mathlesstraveled.com/?cat=17. I clicked on the link for books on the right hand side and read through some of his postings. He has found some books that seem not only interesting but also humorous that could be used in class, or if nothing else at least added to our list of books in Dr. Wright’s class. Not only does he have posts on new books but if you scroll down far enough you can see on the right his virtual bookshelf. Just realize, though, that not all of them are meant for a middle or high school classroom.
I think another thing I’d really like to shed light on is a great teacher here in River Falls at Meyer Middle School. She actually doesn’t teach math. She teaches language arts; however, you MUST check out her website and the awesome products her students are creating. I guess in my opinion, we math teachers could make math just as cool as she is making language arts if we let our students have fun and blaze their own trail with it. The website is: http://www2.rfsd.k12.wi.us/meyer/teachers/MrsReid6/Home.html. Check out the Podcasts, Student Videos, and Blogs. If these don’t spark any ideas on ways to incorporate these types of technology into your classroom hopefully you will at least be able to remind yourself of what our students (especially middle school student but high school students too) are like: immature and silly but still extremely smart and excited about learning as long as we can bring it to their level and spark their interest.
Completing the square is hard because it has a lot of small steps that have to be put together, and it’s hard to remember what you’re doing unless you understand it well (and you practice). Sam Shah at Continuous Everywhere but Differentiable Nowhere shared his successful strategy for teaching this. It doesn’t look flashy, but if you read through it, you’ll see that it’s a very careful sequence: starting with easy stuff, and building little by little the completing the square algorithm (and all along the way, the students are doing the work–it’s not him doing a show-and-tell lesson). And hey, it worked!
I have become a great Kate Nowak fan since discovering her blog f(t) a few months ago. You’ll probably notice this as a theme in my posts in the next few weeks. Anyhoo… she shared her most recent strategy for introducing logs (I think you’ll like it–it might be as good as the Casci swoosh). She also shared her whole logs unit (cool stuff) check it out!
Sometimes when you are teaching something the first time–or even the second–you want a really concrete way of showing what’s going on. I really love how Carolyn’s lesson on factoring polynomials using fractions tiles worked (go read it right now!).
There are two things I see that made the lesson work really well: one is that she started with numbers, and made the connection that factoring with numbers and factoring with polynomials were really finding the same sorts of things, geometrically as well as algebraically. Then she provided good problems (not all polynomials can be factored easily with algebra tiles), and gave the children a chance to make their own connections between the tiles and the pencil and paper work. I find that one of the most effective things to do when starting out with a new skill like this is to work several problems in parallel: do the tiles, and then do the same thing with symbols.
It’s hard to find the right balance because there’s never enough time for everything, but with foundational skills like factoring, it can really pay off later to make extra practice time so that students feel confident. I homeschooled my daughter for 8th grade, and when we did factoring, and again when we did completing the square, I assigned problems for a couple of days and then asked: should we go on now, or do you feel like you need more practice on this first? And we ended up spending a whole week or more on those topics.
So, there’s this thing about WordPress blogs. What they look like is determined by the “theme” that you install in the blog, and you can totally change the look of the blog in about 5 minutes by installing and activating a new theme. Anyway, suggestions for themes are welcome.
Fractions are the bane of every middle school and high school teacher’s existence, I think. Adrienne Stuckey of Education Adaptations writes that a lot of the students she works with are at a disadvantage because they don’t know their multiplication facts well enough to make factoring easy. (You notice this problem when students are learning to factor polynomials too).
Students learn how to manipulate fractions in 6th grade in this area usually, but by oh, say, 7th or 8th grade, they seem to have magically forgotten everything they ever knew. There are lots of good ways of using manipulatives and diagrams, and things when you first teach fractions, but you want something different when you know you’re teaching it for the second or third or fourth time. Ms Cookie at Ms Cookie at Math Teacher Mambo came up with a fraction song for her students (scroll down to the post titled Fraction Song). It won’t solve the factoring problem, but if you learn it in December you can go caroling to the other math classes ; )
When figuring out how to do your practice computer assignments, do this:
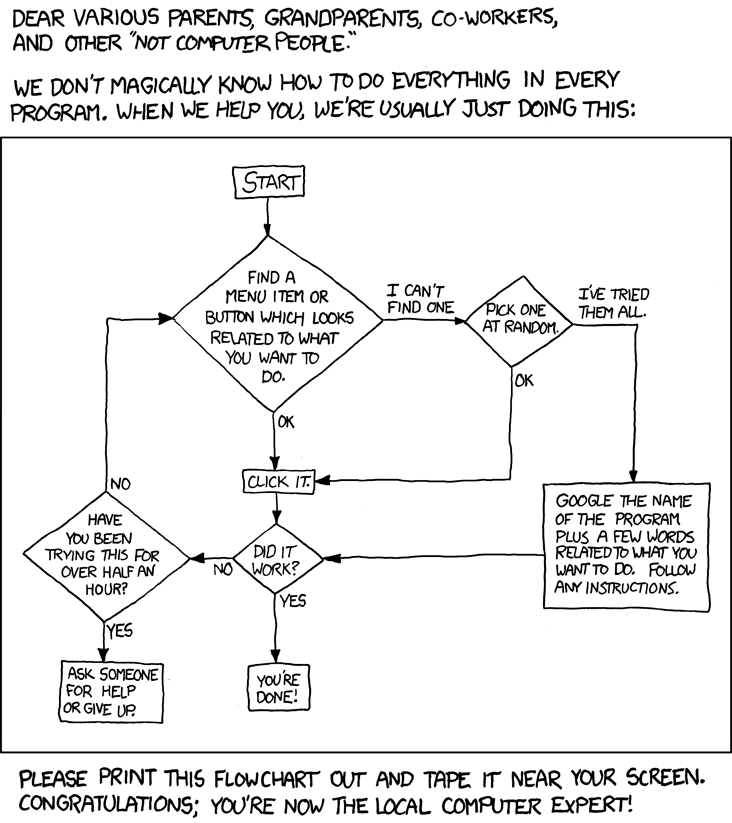
from xkcd
I’m trying out Google forms.
Please take my survey, so I can see how it works