Vocabulary reminder:
dividend ÷ divisor = quotient (with remainder or with fractional amount)
17 ÷ 8 = 2 R 1 or 2 1/8
Which corresponds to
2 × 8 +1 = 17. Or (2 1/8) × 8 = 17
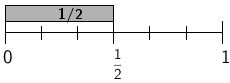
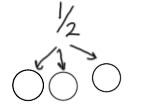
The word problem How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? fits the division problem: 1/2 ÷ 3. That means the interpretation of 1/2 ÷ 3 is 3 people sharing 1/2 lb of chocolate, or, more generally, 1/2 split equally into 3 parts. This is a partitive division interpretation, and it's an easy way to think about dividing by a whole number.
 |
 |
There are 3 parts in 1/2, so there are 2 × 3 parts in the whole, so each part has size 1/6. Each person gets 1/6 lb of chocolate.
Try it:
Write it out for these fractions, then check your answers by watching the video. Keep your note pages--you'll be turning those in as your assignment for this lesson.
CCSS.Math.Content.5.NF.B.7b Interpret division of a whole number by a unit fraction, and compute such quotients. For example, create a story context for 4 ÷ (1/5), and use a visual fraction model to show the quotient. Use the relationship between multiplication and division to explain that 4 ÷ (1/5) = 20 because 20 × (1/5) = 4. (Word problem example from 5.NF.B.7c: How many 1/3-cup servings are in 2 cups of raisins?)
The word problem How many 1/3-cup servings are in 2 cups of raisins? fits the division problem 2 ÷ 1/3. So the interpretation of division for this problem is how many 1/3 cup servings are in 2 cups, or, more generally, how many 1/3's fit into 2? This is a measurement division interpretation, and it's an easy way to think about division of a larger number by a smaller number when the quotient is a whole number (no remainder).
A number line works out well for these sorts of problems pretty consistently, so that's what I'm going to show here. Start with a number line that shows the dividend (2) and subdivide it so that you can easily show the divisor on the same number line (cut everything into thirds). Then count or otherwise figure out how many thirds are in 2.
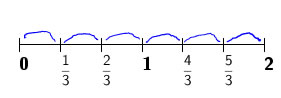
In this specific case of a whole number divided by a unit fraction, you can figure out the number of groups or the number of thirds by multiplying: 2 × 3 (because there are 3 thirds in each whole). Notice that this process corresponds to the invert and multiply algorithm. (3 is the multiplicative inverse of 1.3)
Another way to numerically figure out how many groups without counting is to use equivalent fractions: ![]() There are 6 sets of size 1/3 in 2.
There are 6 sets of size 1/3 in 2.
Try it:
Write it out for these fractions, then check your answers by watching the video. Keep your note pages--you'll be turning those in as your assignment for this lesson.
The measurement division on a number line method that we used for dividing a whole number by a unit fraction also works well any time the divisor is smaller than the dividend and the answer is a whole number quotient (no fractions or remainders).
For example, we can interpret 4/3 ÷ 2/9 as how many sets of 2/9 can be made from 4/3? We can solve it by putting 4/3 on a number line and then splitting each third into 3 parts to make 1/9s. Finally, we can draw and count the sets of size 2/9 in 4/3:

Putting numbers to the process is a little tricker, but this process mimics the number line solution pretty well:
Try it:
Write it out for these fractions, then check your answers by watching the video. Keep your note pages--you'll be turning those in as your assignment for this lesson.