This video is a discussion of this process, and how it applies to products with 2-digit factors.Breaking Apart: It's very helpful to have a and algorithm for solving large multiplication problems--an algorithm is a process (a set of steps) for organizing and finding the solution. In order to understand multiplication algorithms, it's very helpful to know the 1-digit multiplication facts, and it's important to understand how multiplying by 10s affects the product. In the Bassarear textbook, you'll find a discussion of how to break down a product using the distributive law to find the solution (page 177 in the fourth edition).
This video is a discussion of this process, and how it applies to products with 2-digit factors.
Arrays One way to look at and think 2-digit × 2-digit multiplication is to make an array using base 10 blocks. In an array, the 2-digit factors are the lengths of the sides, and the product is the number of square units in the rectangle. Split that rectangle so where the place values of the factors change, and make some trades (10 tens for 100 and 10 ones for 10). The resulting 4 rectangles correspond to the 4 partial products you get from breaking apart the factors as discussed in the breaking apart section.
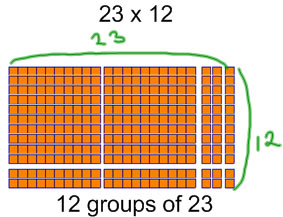
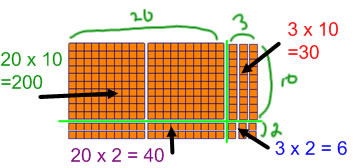
Arrays are a good proportional representation for multiplication for 2-digit × 2-digit multiplication. They can be put together from base 10 blocks, or they can be drawn on grid paper. Ideally, the grid paper provided for drawing these sorts of arrays would have heavier lines on every ten units.
Expanded multiplication
In a 2-digit × 2-digit multiplication problem, if you add up the four partial products that you get by splitting the numbers along place values (as shown in the previous array), that sum will be the total product. The expanded algorithm is the name we give to a way of writing down those partial products vertically below the problem.
This video explains arrays and the expanded algorithm for 2-digit × 2-digit multiplication problems in more detail.
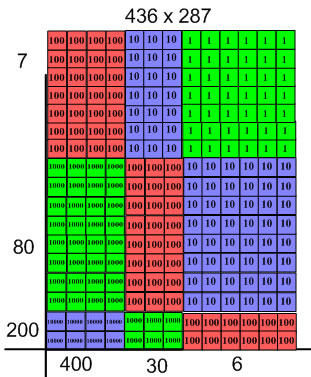
It's difficult to make a proportional array representation of a multiplication problem with a 3-digit factor. If you wanted to use base 10 blocks to make 168 × 273, it would take more than 300 flats, and it would be almost 3 yards long. The problem is that you need to make a rectangle so that a length of 100 units and a length of 1 unit are both visible and easy to work with.
Because it's so hard to manage hundreds and units at the same time in a proportional way, it can be helpful use non-proportional manipulatives or to hand-draw a non-proportional array (labelling rows and columns with place value amounts).
The expanded algorithm, because it works only with the numbers (non-proportional) extends easily to handle 3-digit factors, with only the difficulty that the problems take rather a lot of space.
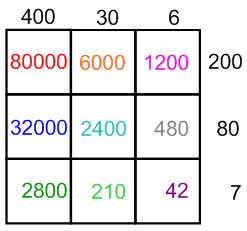
When you split a 3-digit × 3-digit multiplication problem along place values, you should see that in each case you have the same 9 partial products which can be added to find the total product.
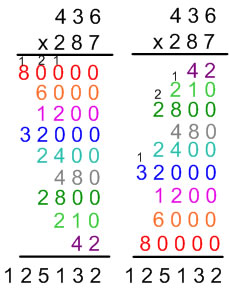
This video consists of a discussion of 3-digit × 3-digit multiplication.
The standard agorithm is similar to the expanded algorithm, but with some of the steps combined. There are two points that can be particularly confusing to children when learning the standard algorithm. I want you to pay attention to how I explain those points, and I want you to think about how you would explain those points. Those particular difficult points are:
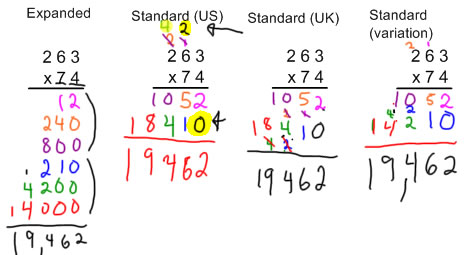
This video discusses the standard multiplication algorithm