The most important thing about a function rule is that it must always give you the right output (no matter what the input). When we figure out what we think the function rule is, we generally use inductive reasoning: we look at a pattern of numbers (often in a table) and try to figure out an algebraic rule that would fit that pattern. In order to make sense of a rule, however, and to prove that it is the correct rule using deductive reasoning, you need to know some properties of the function. I
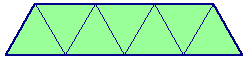
A property of a function rule is sometimes the same as knowing where it comes from. For example, if I know that the function rule is describing the perimeter of a pattern block train, I can use properties of pattern block trains and of perimeters to justify my function rule. For example, with a triangle train, you have the picture:

the table:
| n=# of triangles | p = perimeter |
| 1 | 3 |
| 2 | 4 |
| 3 | 5 |
| 4 | 6 |
and the equation: p = n + 2 (pretty easy to guess from table)
But what does it have to do with the perimeter? Well...
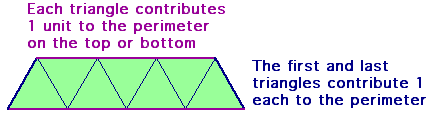
So the top and bottom sections of the perimeter are n long altogether, and the ends are 2 long:
p = n + 2
See a similar example with the trapezoid train
Another property might come out of the step size. A situation like: John starts 4 feet from the tree. If he walks 3 feet every second (away from the tree), how many feet is he from the tree after n seconds? In this case part of the problem situation tells you that for sure the step size is always 3. This is a property that you can use deductively. (When you look at a table and figure out that the step size is 3, you are infering that it will always be 3, and you are inductively continuing that pattern. The difference between this and a deductive property and hypothesis is that with a deductive hypothesis, you are explicitly stating it as a condition of the problem).
The function rule is d = 3n+4
(d=distance from tree, n=# of seconds)
This rule makes sense because after n seconds, he has walked 3n feet*. If he started out 4 feet from the tree, that would make him 3n + 4 feet from the tree.
*When I say that after n seconds at 3 feet per second he walks 3n feet, I am using the definition of multiplication as repeated addition--after n feet, he walks 3 feet n times, which is written 3n.