Making connections between geometric, numeric and algebraic representations of patterns

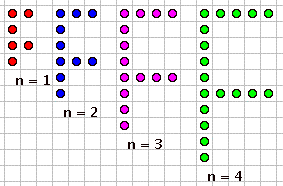
When you have a growing pattern that is shown geometrically, like this one from the WisWeb site, you can make the algebra in the pattern more clear by highlighting certain geometric and numeric patterns.

One thing you do is analyze how the pattern is growing geometrically--where do you add dots to get the next one?

If you can analyze that, then you can draw the next example. In this case, you need to add a dot in 4 places: on each of the horizontal lines of the F, and in top and bottom sections of the vertical line of the F.

Next, you want to look for the number (the step number) in the growing parts of your pattern. This is usually easiest to see with the larger versions of the pattern (and kind of hard to see in n=1), but once you find the right places, you should be able to circle n dots in the same places in each of the examples:

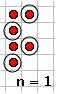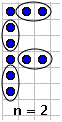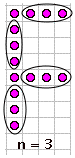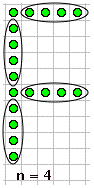Next, we're going to make the connection to the number pattern by writing down the number of dots in each pattern as a sum and a product, paying attention to the dots we circled:

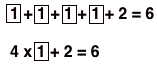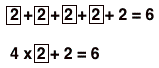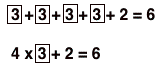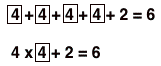Notice that I have the n-number (step number) in a box, and that the boxed numbers correspond to the dots I circled. The goal in doing this is to emphasize how the growing part of the pattern in the picture corresponds to how the numbers grow.

When I make the jump from writing the numbers as a sum to writing them as a product, I also need to remind my students why those are doing the same thing. I might say something like:

Remember that 4 times 3 means 4 threes, so when I have 3+3+3+3, that means the same thing as 4x3

This uses the repeated addition model to explain the multiplication.

Finally, I want to show the general algebraic form of the equation, and I write it in the same way I write the multiplication versions of the numbers:

By writing the numerical versions of this equation several times, I can show how everything stays the same in the number expressions except the boxed number, which matches the step number n. My general algebraic equation is exactly the same as the number expressions I wrote down, except for replacing the boxed number with n, because the boxed number is always the same as the step number (n).

This way of explaining the function rule is both inductive and deductive

It is inductive because the function rule matches the examples:

It is deductive because I am using properties of the geometric pattern to justify my number work and equations: