Different representations of fractions are good for different things:
Comparing
Fraction circles are really good for comparing and ordering fractions. The visual diferences between the sizes stands out better than for any of the other representations. The next best representation for comparing fractions is probably a number line or fraction bars. Both squares and discrete sets can be hard to compare
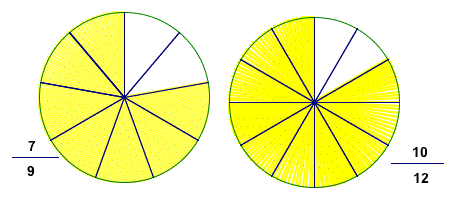
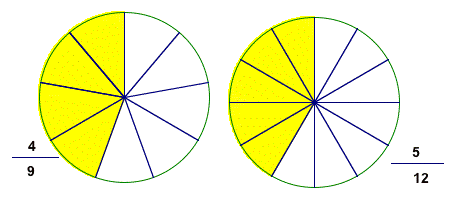
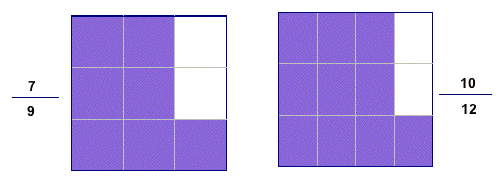
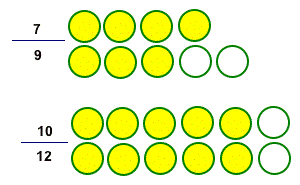
The examples below are showing, respectively, that 7/9<10/12 and 4/9 > 5/12
Fraction circles: which circle is most complete?


I think the appeal for fraction circles for visualization tasks has to do with the way our brains process visual information, so the angles formed in fraction circles are very distinctive.
Fraction bars: which bar is longer?
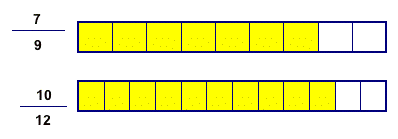
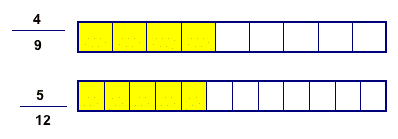
Fraction bars line up very nicely for comparisons.
Some fraction squares are harder to compare than others; Which of these are the hardest?

Fractions of a set: which set has the higher proportion of yellows?
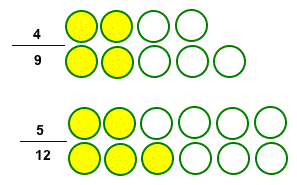
I think fractions of a set are the very most difficult to compare, because your eyes want to compare the amount using whole numbers rather than the proportion which is the fractional amount. For instance: 4/9 is bigger than 5/12, but it's hard to see that in the discrete picture.