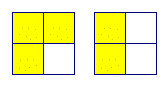
When adding (or doing other computations) where the answer is greater than 1, there is a common confusion over what the whole is. For example, when adding 1/4 + 2/4, students might disagree over whether the answer is 5/4 or 5/8 (and, also, whether 5/4 is an acceptable answer or if the answer must be given as 1 1/4).

Perhaps because of prior knowledge about rulers, students find fractions bigger than one to be easier to accept in fraction bars than in other models:

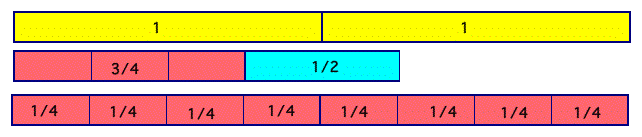
Fraction bars can be lined up nicely and compared, so you have visual confirmation that the sum is indeed greater than 1, and that you can have more than 4 fourths.

The big idea, however, remains the importance of knowing what your whole is. If you are clear in your representation of what 1 is, then it is possible to decide what the answer should be