Classifying triangles:
This discussion is aimed at a Van Hiele level 1-2 understanding, and thus is fairly sophisticated for elementary students. This set of problems shows the sorts of thinking we want students to develop to be ready for High school math. Most of this work with triangles is appropriate for students grades 3 and above.
There are 6 special named types of triangles: scalene triangles, isosceles triangles, equilateral triangles, right triangles, acute triangles, and obtuse triangles. Here are their definitions:
The first 3 are usually defined by side length properties:
Scalene triangles have all 3 sides different lengths
Isosceles triangles have at least 2 sides the same
Equilateral triangles have all 3 sides the same
The second 3 are defined by angle properties:
Right triangles have one angle that is equal to 90°
Acute triangles have all 3 angles less than 90°
Obtuse triangles have one angle that measures more than 90°
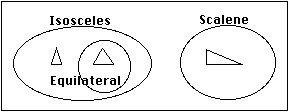
Notice that if you have all 3 sides the same length, you automatically have at least 2 sides the same length. If you have no sides the same length, however, you can never have two sides the same length, so we can show the relationships between equilateral, isosceles and scalene triangles this way:

Equilateral triangles are a subset of isosceles triangles, because every equilateral triangle is also isosceles (though some isosecles triangles are equilateral and some are not). Isosceles and Scalene triangles are disjoint sets--they don't overlap at all because a triangle can never be both isosceles and scalene.
Practice problem--how are right, acute and obtuse triangles related?
A good exercise for beginning to think at the analysis level (Van Hiele level 2) is to consider when a triangle can have both a side length and an angle property. For example: can you have an isosceles right triangle? Try it with this applet, and see if you find one that works (remember, to be isosceles, two sides must be the same length, and to be right, one angle must be 90°).
Finding all of the ways that you can and can't combine an angle and a side length property is an appropriate task for encouraging students to do higher level thinking, and can be done as early as third grade if students have appropriate concrete manipulative tools to help them experiment with triangles. I found an isosceles right triangle, and I have entered it in a table to find all of the possible combinations. You may find the other possible triangles as part of an assignment or exploration:
| Scalene | Isosceles | Equilateral | |
| Right | 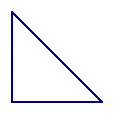 |
||
| Acute | |||
| Obtuse |
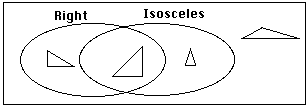
A more advanced way of thinking of the relationships between types of triangles is with a Venn diagram (This could be used in presenting material to intermediate grades students, and of exploring with middle grades students)
In this case, the sets overlap. I have shown an example in each region, because there is one: there are triangles that are both right and isosceles, right and not isosceles, isosceles and not right, and triangles that are neither right nor isosceles (it helps to know that if a triangle isn't isosceles, it must be scalene, so "right but not isosceles" means the same as "right and scalene):