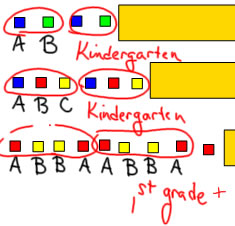
K-1 patterns
When children first work with patterns, they work with repeating patterns where the pattern is fairly short (usually 2 or 3 in length) and not too tricky. For example, the AB and ABC patterns are simple enough for kindergarten children to understand, but the length 4 ABBA pattern is extra tricky (because it begins and ends with the same thing) and it's a bit long--it's harder to hold a pattern of length 4 or 5 in your head than a pattern of length 2 or 3.

When you're showing a pattern to children, it's important to show enough for them to be confident that they know how the pattern goes. When working with repeating patterns a good rule of thumb is to show at least 2 full repetitions.
Children in kindergarten can understand patterns well enough to tell what comes next in a pattern, to build onto a pattern and to make repeating patterns of their own.
Questions about repeating patterns (patterns in grades 1-3)
An activity to get children thinking about what comes next in a pattern is to make a pattern with counters and cover up some of the counters with cups or something similar. Leave at least the first two repetitions uncovered and ask what comes next? or point to a cup and ask: what color is under this cup? Children in K-1 can usually figure out the hidden counter by pointing to or touching the cups and reciting the pattern as they go:
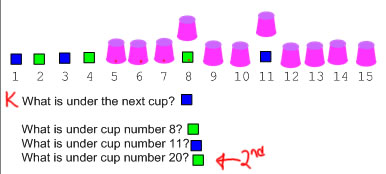
By second grade, children can figure out the hidden counters for a few steps beyond the end of the cups. An AB pattern like this one is easier, of course to figure out because the colors correspond with odd and even numbers. With an ABC pattern or this AAB pattern, it's more complicated, because you need to know things like multiples of 3:
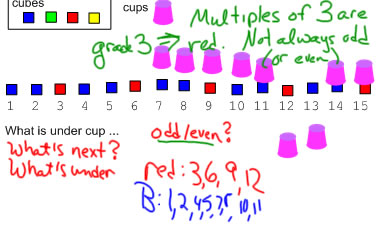
Repeating patterns can make a good bridge to skip counting for children in grade 3 and 4. With an ABC pattern like this (or any pattern where each letter is used only once) the question of which numbers go with a given color produce numbers in a skip count pattern:

By giving a pattern to follow for the skip count sequence, it ties skip counting to a something more concrete. Children have a more concrete (draw the sequence) and a more abstract way of finding the sequence of numbers (skip counting or repeated addition). By extending the amount of the sequence you ask for with numbers beyond the spaces for the pattern on the page, it encourages children to find and use the more abstract pattern, while giving them a visual way to understand what the pattern is and does.
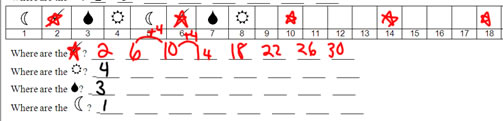
By asking for the skip count patterns for different shapes in a jumbled up order (star, sun, raindrop, moon rather than the order they appear in the pattern), it encourages children to keep using the order of adding 4 as they go across rather than adding down in the columns. (There are other learning goals for which it would be a good idea to use the order that the symbols appear in the sequence)
This skip counting skill and strategy is important in grade 3 and 4 as a way to understand and compute multiplication.
Skip counting skills, once they are introduced and understood can be effectively practiced in more abstract contexts. Some examples are...
| the sorts of skip count problems you find on standardized tests: | 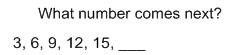 |
| or skip count puzzles: | 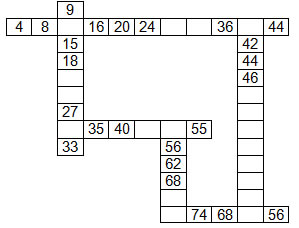 |
In higher grades (4-8), children's work with patterns changes from repeating patterns to growing patterns. At the concrete end of what children do, there's a lot of overlap with what children can and are expected to do in grades 2-3. Many growing patterns can be represented concretely with pattern blocks, and abstractly with skip counting patterns. One example is these pattern block trees:
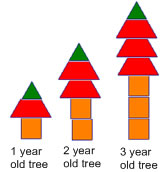 |
The first thing children should do with a pattern like this is to make sure they understand what the pattern is, and how it grows. The most concrete way to do this is to build the next "tree" in the pattern with their pattern blocks. Children as young as kindergarten can do this for patterns that grow in a simple way. |
To make the numerical growing pattern that is associated with this pattern block pattern, we can ask children to collect and represent information about how many blocks are in each tree in a table. In the table children can tell how many pattern blocks in all for each tree, or they can tell how many pattern blocks of each type (how many squares, trapezoids and triangles):
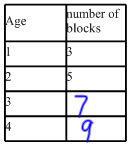 |
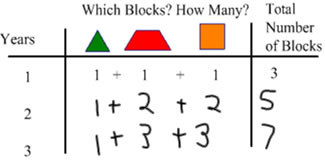 |
Third, fourth and fifth grade-level problems ask children to extend and reason from the visual and numerical patterns they find to make predictions about later stages of the pattern.
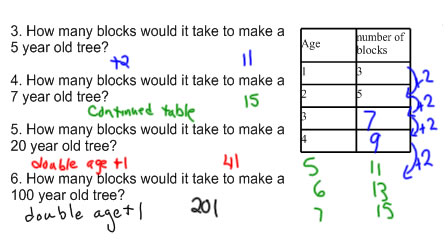
Third grade children should be able to extend the skip count pattern in the table to figure out how many blocks it would take for the next several stages of the pattern (perhaps up to 10 year old tree it's reasonable to solve these problems by extending the table).
Some children in grade 3, and most children in grade 5 will be able to find the other pattern here, that the number of blocks is double the age of the tree +1. This second is more obvious in this case if you use the table that is broken out by pattern block shape.
 |
In each year, you have that many trapezoids and that many squares and only 1 triangle, so a 20 year old tree would have 20 trapezoids, 20 squares and 1 triangle, which makes 41 total blocks. |
Multiplication
The second kind of thinking about this problem is multiplicative. When you see part of the pattern as "double the age", you are seeing it as multiplication: 2 × age. This fits with the pattern block break-down pattern too. If the age is N years, there are N trapezoids and N squares, so there are N+N together, and N+N means N taken 2 times--2×N. Putting a pattern like this into words (double the age plus 1) and symbols (2×N+1) is something that should be introduced and discussed increasingly in grades 3-5.
Another type of pattern block pattern that you may find in third grade materials is one with a repeating pattern for the pattern blocks, but the questions are growing pattern type questions about the number of blocks. For example, if you make a pattern block "train" with train cars like the ones shown below, you can ask questions about trains with a given number of cars
The pattern:
|
The questions: |
This is a very multiplicative pattern--there are 3 blocks in each car, so if you know how many cars there are, then you can multiply by 3 to find out how many blocks there are total. If there are N cars then there are N sets of 3: N×3 blocks. There are also 2 blue rhombi on the sides of each triangle, so if you know how many green triangles, you can double it (2×N) to find out how many blue rhombi you need.
Children can recognize and continue patterns that are simple enough for them to understand.
Making predictions about what comes next and what comes later in a pattern develops reasoning skills for understanding, representing, and relating numbers to patterns.
Patterns can give children a concrete way of thinking about skip counting and other numerical patterns.
Skip counting is an important skill for children to develop and reason about in third grade.
As children practice skip counting in a variety of contexts, they develop and extend their understanding of multiplication.