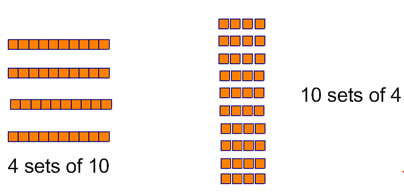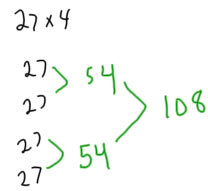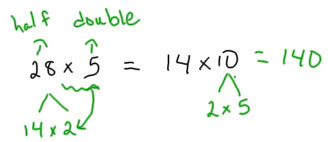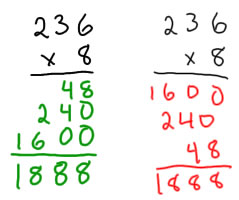The commutative law helps us out when first learning about multiplying multi-digit numbers. It's easier to think of 10x4 as being 4 sets of 10 than of 10 sets of 4:
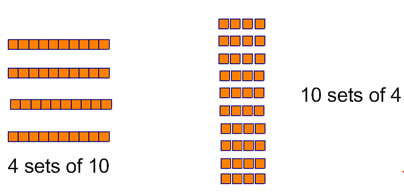
4 sets of 10 is better because we group by 10's in our number system, so grouping into sets of 10 is more helpful that grouping into sets of 4. It's important to understand place value to understand this, and it's also important to understand the commutative law of multiplication, so that you can interpret both 4x10 and 10x4 as 4 groups of 10.
For this lesson, we're going to look at multiplying numbers where one of the numbers--which we'll treat as the multiplier--is a single digit number, and the other number--which we'll treat as the multiplicand--is a 2 or 3 digit number.
The first thing to learn is how to multiply when the multiplicand is a multiple of 10 or 100. We'll start by showing the multiplication using base 10 materials. These diagrams show 5x30 with a proportional (base 10 blocks) and a non-proportional (Montessori stamp game) material. In both cases, 5 is the number of groups, and there are 30 in each group.
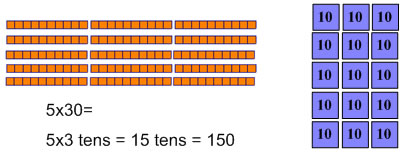
A great way to think about and describe what's going on is to say that 5 sets of 30 is 5x3 tens= 15 tens (like the thought bubble on page 82 of Primary Mathematics 3A). When you turn 30 into 3 tens you make it easier to see the problem 15x3 as just the problem of figuring out 5x3 with "tens" telling you what you have 5x3 of (you have 5x3 tens).
If you look at the diagrams in the Van de Walle text, you will see that he favors base 10 blocks as a standard representation, and if you look at the Primary Mathematics 3A diagrams (pg 82), you will see that they are representing it with a non--proportional material. Proportional materials, as you may recall, have the advantage of helping children see relative sizes of numbers more effectively, and an advantage of non proportional materials is that you can show and solve problems with larger numbers without running out of space (I could show 80x5 with the non-proportional materials much more easily than with proportional materials). Children in third grade should have done enough work with place value that they can work with either kind of materials effectively.
Children should first practice with problems where one number is a multiple of 10 or 100 like those in problems 1-3 on pages 83-84 of Primary Mathematics 3A. After they get used to the patterns and thinking you do for multiples of 10 and 100, it's time to put those values together, and multiply larger numbers (still by just a single digit multiplier).
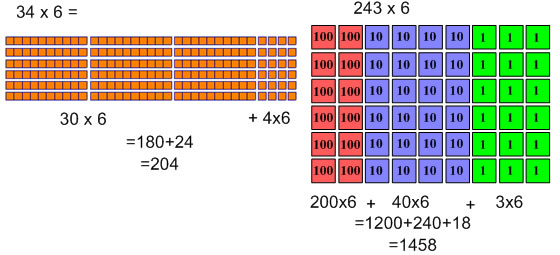
Multiplying 2 and 3-digit numbers by single digit numbers can be represented well using the distributive law--think of multiplying in each place value and then adding those values together. This works well with a representation with manipulatives:
Informal algorithms
Children, if given problems at a level that's appropriate for them, will develop ways to keep track of the parts of problems like these. Van de Walle shows several of these on page 174. All of these strategies show an understanding of multiplication by students, and show developing number sense.
The complete number strategies, and strategies of partitioning the multiplier show that the child understands that multiplication can be computed by repeated addition, and that the child has good mental math strategies for adding large numbers.
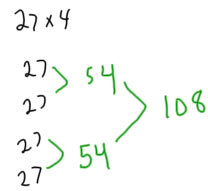
The compensation strategies on page 175 show, respectively, an undrestanding of how multipliers are related (distributive law--on left), and how halving and doubling are related (a specific case of multiplication and division or breaking apart a factor--the associative property).
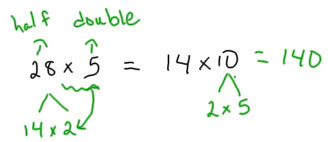
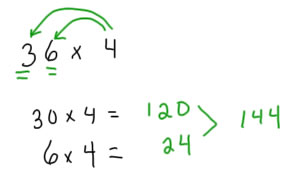
The strategies that are best for generalizing and using for all multiplication problems are the decade partitions. Children who partition multiplication into decade numbers and can work easily with decade numbers have a good groundwork for expanding to bigger problems (usually 4th grade) and developing or learning efficient strategies for multiplying all numbers.
Expanded algorithm
All of the important ideas for multiplication can be represented with the expanded algorithm. In this algorithm, each of the place values is computed and written separately, and then those partial products are added. In this algorithm it's OK to write the partial products in any order, so long as you have them all.
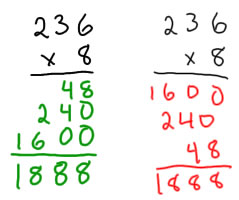
Traditional algorithm
The traditional algorithm is a way to collapse the expanded algorithm so that it takes less space by recording the highest digit as a "carry" number. In different countries, these digits numbers may be written in different places.
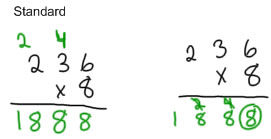
When and if you teach the standard algorithm, try to keep using the place value language that you apply when talking about multi-digit numbers with manipulatives and addition and subtraction: the second multiplication isn't 8x3, it's 8x30 or 8x3 tens, and when you carry the 2 from 24 tens, that isn't just a 2, it stands for 2 hundred.
Lattice algorithm
The lattice algorithm is a way to collapse the expanded algorithm where the "carry" numbers are recorded in a lattice that you draw before starting the problem, so that they stay organized and end up in the right place at the end.
I can't say I've done extensive research on this, but I think that the lattice multiplication must have been in use in England in the 1500's because John Napier who invented logarithms (which you may remember from high school) also invented a manipulative-type tool for multiplying that uses a lattice structure. If you look at where the digits that are carried go in the second version of the standard algorithm (that's how they teach you to write it if you go to school in England), you'll see that it's pretty similar to where the same digits are in the lattice algorithm.
The trickiest part about the lattice algorithm is that you have to get it all set up neatly before you start--you need your digits spaced out right so you can fit a lattice (a box with a diagonal drawn in) underneath each digit. Then when you multiply 8 by the digits in 236, the products fit in the box underneath the appropriate digit and the spacing of the lattice takes care of getting everything in the right place value.
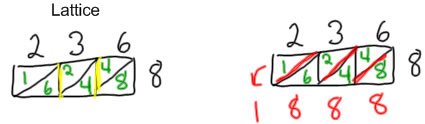
When you are multiplying out the digits--the partial products, you pay attention mostly to the lattice lines going down--the product lines up under the digit you're multiplying by. The next step is to add--that's where the "carry" digits get added in--and for that step, you pay attention to the diagonal lines, and those bump each digit over into the correct place value to get added in, and it ends up looking a little bit similar to where the carried digits end up in the English version of the standard algorithm.
Everyday Math uses the lattice algorithm, as one of the multiplication algorithms it teaches, so you may see this one again.
All of the standard/named algorithms have a similar structure in that you multiply, keeping everything in the correct place value, and then add up the place value products. In the standard/traditional algorithm, you add things as you go along so that it is as compact as possible (takes up a small amount of space). In the expanded and the lattice algorithm, you add up the place value products at the end. All of these algorithms are similar to the invented decade-partition method and they are similar to what you do if you are using place-value manipulatives.
