
In this lesson we look at multiplication and division through the lens of repeated groups and repeated addition.
The CGI organization splits out 4 different sub-types of repeated grouping multiplication and division. Our goal in this lesson will be to see how these 4 sub-types are similar to each other, and distinguish multiplication from division, and the two different types of division from each other. We'll also look at how to represent multiplication and division using discrete objects (counters) and using a more continuous model (bar diagrams/Cuisenaire rods).
The first way we understand and learn about multiplication is as repeated addition: the amount in several sets, each of which are the same size.
Grouping
The most accessible version of having repeated groups is to have a problem that describes physical groups, each of which are the same size.
Example: A bee has 6 legs. How many legs do 5 bees have?
(note: this is the problem discussed by the children in the kindergarten clip on the CD that accompanies Children's Mathematics)
In this problem there are clearly 5 sets of 6 legs--one set of 6 legs for each bee. This problem lends itself well to a direct modeling approach: it's clear how to represent this problem with 5 sets of discrete things that you can count. One diagram might look like this:
This representation shows each leg separately, and is related to the sort of representation children might make with counters:
Knowing that this corresponds to 5 sets of 6, or 6+6+6+6+6 tells us that this is a multiplication problem. One of the fundamental notions that multiplication is built on is repeated addition, and all of our later ideas of multiplication have to fit in with (be consistent with) that interpretation. So 5x6 means "five sixes" or "six taken five times").
A bar diagram is another representation for 5 sets of 6 that is more abstract because the 6 items are not represented individually

Vocabulary:
There are two different sets of words we use to describe the parts of a multiplication problem. The words we use when describing multiplication in the way that a K-1 or K-2 student sees is are:
multiplier x multiplicand = product
The multiplier is the number of groups. The multiplicand is the amount in each group or the size of each group. The product is the total of everything in all of the groups together.
Later, we'll look at why you can switch around the numbers in a multiplication problem (the commutative property), and then we'll use other words to describe the numbers in a multiplication problem. This fits better with the way we want children to think of multiplication in higher grades (3 and above):
factor x factor = product.
Price
Example: A pencil costs 8¢. How much do 3 pencils cost?
You can think of a price problem as a grouping problem (3 groups of 8), where the amount in each group is the price for 1 item, and the groups correspond to the items.
Rate
Example: Jake earns $4 an hour raking leaves. If he rakes for 3 hours, how much will he earn?
Rate problems (miles per hour, dollar per hour, etc.) are inherently comparitive, ratio statements--they are talking about a relationship between two measurements. Rate problems are often introduced later than the grouping and price problems (grade 3-4 rather than 1-2).
In this example, the rate is $4 per hour. A bar diagram showing 3 hours at $4 per hour would look like this:
The amount per hour ($4) is the amount per group in this case, and the number of hours corresponds to the number of groups. This is 3 groups of 4.
Multiplicative Comparison
Example: Sarah has 5 Silly Bandz.
Amy has 3 times as many Silly Bandz as Sarah.
How many Silly Bandz does Amy have?
The multiplicative comparison part of this is the "3 time times as many [...] as [...]". This specifically describes a multiplication relationship: 3x[the number Sarah has]. While in some ways, this just tells you what to do, it's still a pretty complicated sentence structure.
A typical diagram for this problem is a bar diagrams with two bars (to show comparison):
Since the question asks for the amount Amy has, we find this by computing 5+5+5=3x5: 3 groups of 5.
The reason for showing two bars is that we are comparing Sarah's amount to Amy's not saying that Sarah's amount is a subset of Amy's.
If you look for how this fits into a grouping structure, you'll see that Sarah's amount is repeated, so that's the size of a group. Amy has 3 times as many as Sarah, and that "3 times" tells how many groups.
There are essentially two ways of thinking of division:
Partition division (also known as partitive, sharing and grouping division) is a way of understanding division in which you divide an amount into a given number of groups. If you are thinking about division this way, then 12 ÷ 3 means 12 things divided evenly among 3 groups, and we wish to know how many is in 1 (each) group.
Measurement division (also called repeated subtraction division), is a way of understanding division in which you divide an amount into groups of a given size. If you are thinking about division this way, then 12 ÷ 3 means 12 things divided evenly into groups of 3, and we wish to know how many groups we can make.
Partitive: I have 12 cookies. I want to put them on 3 plates, so that I have the same number of cookies on each plate. How many cookies should I put on each plate?
Dividing 12 by 3 in a partitive way involves taking 12 objects and "dealing" them out evenly into three groups. Typically each counter is moved separately, and this takes 12 steps:
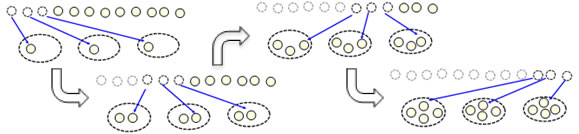
Measurement: I have 12 cookies. I want to put 3 cookies on each plate. How many plates do I need to hold my cookies?
Dividing 12 by 3 in a measurement way involves taking 12 objects and making groups of 3 from them. With a small number (3) in each group, this is typically a faster process because 3 counters are removed at a time, so this might take only 4 steps.
Multiplication: I have 4 plates. Each plate has 3 cookies. How many cookies do I have in all?
Multiplying 4x3 involves making 4 groups of 3 and counting all of them. Some children will make groups of counters where the groups are identified by the arrangement, and some children will use a counter to designate the group:

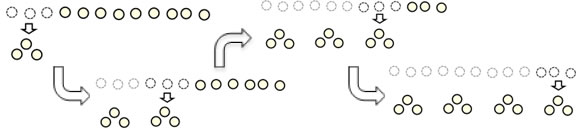
Partitive: I have 24 cookies. I want to put them on 3 plates, so that I have the same number of cookies on each plate. How many cookies should I put on each plate?
The diagram for a partitive division situation shows the groups as equal sized parts of a bar and the amount per group is written in to the bar. In partitive division, we don't know the amount per group, so that is represented with a "?".
If you try to solve a problem like this with the Cuisenaire rods, you'll find that you need to guess and check to figure out which rod is the right size to use for the problem:
Measurement: I have 24 cookies. I want to put 3 cookies on each plate. How many plates do I need to hold my cookies?
The diagram for a measurement division situation shows the size of the bars, and we have to figure out how many of them to make the right length. The "..." (my English-major husband tells me these are called ellipses) are a stand in for an an unknown number of bars that we need to make 24 in all.
It's little easier to solve this one with Cuisenaire rods than the last one, because we know which rods to use (the 3's), we just have to keep adding more until it's the full length of 24.
Multiplication: I have 3 plates. Each plate has 8 cookies. How many cookies do I have in all?
Multiplying 4x3 involves finding the total length of a bar showing 3 sets of 8. Notice that the thing that's different about this from the partitive division problem is the unknown--this time "?" is denoting the total.
The Cuisenaire rod work is straightforward because we know what to start with (four 6-rods), and we only need to find the total
Examples with price problems:
a. 4 pencils cost 36 cents. How much does one pencil cost?
b. A pencil costs 8 cents. How many pencils can I buy for 24 cents?
c. A pencil costs 10 cents. How much do 4 pencils cost?
With a price problem, the items--in this case pencils--correspond to the repeated sets, and the cost per item corresponds to the size of the set.
a. 4 pencils cost 36 cents. How much does one pencil cost?
Partitive division:
|
b. A pencil costs 8 cents. How many pencils can I buy for 24 cents?
Measurement division:
|
c. A pencil costs 10 cents. How much do 4 pencils cost?
Multiplication:
|
Examples with rate problems:
a. A toy train goes 4 inches in 1 second. How far does the train go in 5 seconds?
b. A toy train goes 6 inches in 1 second. How long will it take for the train to go 24 inches?
c. It takes a battery powered toy train 5 seconds to go 20 inches. How far does the train go in 1 second?
In a rate problem, the rate relationship indicates where the repeated sets are. In this case the rate is a number of inches per second. The seconds correspond to the repeated sets, and the number of inches per second corresponds to the amount in 1 group.
a. A toy train goes 4 inches in 1 second. How far does the train go in 5 seconds?
Multiplication:
|
b. A toy train goes 6 inches in 1 second. How long will it take for the train to go 24 inches?
Measurement division:
|
c. It takes a battery powered toy train 5 seconds to go 20 inches. How far does the train go in 1 second?
Partitive division:
|
Examples with multiplicative comparison problems
a. A farmer has 3 times as many chickens as ducks. He has 18 chickens How many ducks does he have?
b. A farmer has 6 ducks. He has 3 times as many chickens as ducks. How many chickens does he have?
c. A farmer has 6 ducks and 18 chickens. How many times as many chickens as ducks does the farmer have?
In a multiplicative comparison problem, there is a description of a multiplicative comparison: a sentence of the structure: "__ times as many ____ as ____". This number is the multiplier: it corresponds to the number of sets. The amount per set (multiplicand) corresponds the the size of the set that is being compared to: this is the set whose name comes after the word "as" (in this case the number of ducks). The total corresponds to the size of the set being compared (described in terms of the other set): this is the set whose name comes before the word "as"--so the compared set is made of repeated sets whose size is the size of the set being compared to.
That's was a really tangled sentence. Let's try it again with Ducks and Chickens: The multiplicative comparison says that there are ___ times as many chickens as ducks. The number of times takes the place of the multiplier, the number of chickens takes the place of the total, and the number of ducks takes the place of the amount per set. As a repeated set, we can think of the chickens as being made of ___ repeated sets, each of which has the same size as the set of ducks.
a. A farmer has 3 times as many chickens as ducks. He has 18 chickens How many ducks does he have?
Partitive division:
|
b. A farmer has 6 ducks. He has 3 times as many chickens as ducks. How many chickens does he have?
Multiplication:
|
c. A farmer has 6 ducks and 18 chickens. How many times as many chickens as ducks does the farmer have?
Measurement division:
|
Notice that multiplication and partition division examples have very similar wording, because they both have the multiplicative comparison statment: "[the farmer] has 3 times as many chickens as ducks", which is a description of the relationship in size between two groups--the total, and the comparison group. The measurement example is worde quite differently, and indeed is kind of awkward.
A key to understanding multiplicative comparison problems that include a comparison (such as "[the farmer] has 3 times as many chickens as ducks"), is to realize that the comparison group takes the place of the unit groups in grouping problems. So, the number of ducks becomes a comparison group that lets you group chickens into groups that are as big as the duck group.
Thus, in a multiplication problem, you are told the amount in the comparison group, and you consider 3 groups of chickens, each of which has the same number as the amount of ducks--3x6.
In a (partition) division problem, you are told the total number (of chickens) and once you partition them into 3 equal groups you can find out what size one group of chickens is, and that is the same as the number of ducks. If you imagine doing this by direct modeling, you can see that you would be doing the same process when you split the chickens into 3 groups as you do in a grouping partition division problem.
In the measurement division problem, what you are looking for is the multiplicative comparison. You need to know how many times the total number of chickens is when compared to the comparison group of ducks. If you imagine direct modeling this, you would be making groups of 6 chickens, and then you can see how many groups of 6 corresponds to the total of 18 chickens.