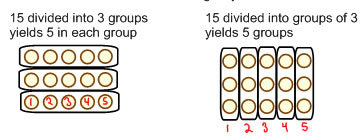
notice that the same array diagram the shows us the commutative law of multiplication also shows us this relationship between the two ways of thinking about division.
Usually the first experiences we give children with division are with numbers that can be evenly divided. There's are two really important principles that children should be exposed to with numbers that can be evenly divided.
notice that the same array diagram the shows us the commutative law of multiplication also shows us this relationship between the two ways of thinking about division.
15 ÷ 3 = 5 15 ÷ 5 = 3 3 × 5 = 15 5 × 3 = 15
Division being the inverse of multiplication is fairly natural, because most division interpretations and word problems are all about repeated groups. Understanding this relationship is in the third grade Common Core standards, and as a third grade teacher, you would help students make the connections between division and multiplication. The first development of this idea should come from contexts and word problems and diagrams showing division as repeated groups.
After division has been associated with repeated groups through word problems and/or manipulatives, we start showing children how to write down fact families (like the one above) for division problems, and writing missing number multiplication problems to solve division.
| Fact family for 15 ÷ 3 | Missing number multiplication problem for 15 ÷ 3 | ||||
|
3 × ___ = 15 |
When we're figuring out the answer to a divison problem using mental math (without manipulatives/direct modeling, but before having the division facts memorized) there are a few ways that work well to divide:
Partitions?:
Halving works: Splitting a number into two equal parts works well for a lot of people. I can figure out how much half of 8 or 12 or 48 is without too much trouble. You can split a number in half once and then split it again to divide by 4. These ways of figuring out a division solution work with thinking of dividing in a partitive way: you want to split into 2 or 4 equal groups.
Splitting a number into 3 equal parts is a lot harder. I can reorder 6 random items into 3 groups of 2 pretty easily in my mind, but anything larger than 6 gets pretty hard. Try to visualize (without drawing or acting out) what it would look like to have 12 objects and to move them around into 4 equal groups. I think it's pretty hard, and so do a lot of people, so a partitive model doesn't help me very much for dividing by 3 if I'm trying to do it mentally without using something I've memorized (multiplication facts, for instance, would be very helpful here--solving 3 × ___ = 12 is rather easier).
For an example of how a partitive division divided by three problem is hard, please pull out your "Childrens Strategies" CD from the Children's Mathematics (CGI) book. Watch the Multiplication and Divison, Counting Strategies, Measurement Division clip and then the Partition Division clip. You should be able to tell that it's the same student solving both problems--first the measurement division problem and then the partition division problem.
----watch the clips and then read on----
Notice that when she was solving the measurement division problem, she successfully skip counted by 3's up to 21, and deduced that there were 7 groups (great skip counting skills!)
When she was solving the partition division problem, she did something that you probably didn't follow. Read my description and then go back and watch her again.
Stuff she knows:
Stuff she doesn't know:
Knowing that partitive division and measurement division strategies give you the same answer is a pretty powerful thing. It can be thought of as a combination of knowing that division means the same as missing number multiplication, and knowing the commutative law of multiplication.
Measurement division?
Skip counting: Skip counting (and tracking the number of groups to find the answer) is a very flexible way of using mental math to solve division problems. It comes naturally for measurement division problems. It takes a while to learn that the answer you get from skip counting also works for partition division problems. Skip counting works for dividing any number that's not too big by any number you can skip count by.
Think multiplication: If you know your multiplication facts, the winning move for division is to use those multiplication facts. If you are asked for 21 ÷ 3, you can turn it around into 3 × ___ = 21, and use your knowledge of multiplication facts to figure it out!
The inverse of multiplication
Not all division problems give you a whole number answer. Division with remainders gives you the closest multiplication that is less than the dividend, and then you add on the remainder:
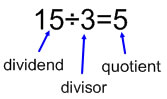
When we divide, the amount that is being divided up is called the dividend. In 15 ÷ 3 = 5; 15 is the dividend, 3 is the divisor and 5 is the quotient |
 |
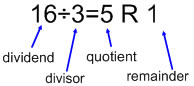
If there is the remainder, then the other parts of the equation keep the same names, but a remainder is also added on at the end. In 16 ÷ 3 = 5 R 1; 16 is the dividend, 3 is the divisor, 5 is the quotient, and 1 is the remainder |
 |
The division 15 ÷ 3 = 5 corresponds to the multiplication 3 × 5 = 15 The division 16 ÷ 3 = 5 R 1 corresponds to the same multiplication because when multiplying by 3, 3 × 5 is the closest you can get to 16 without going over 16. The equation that shows how the numbers are related by multiplication is: 3 × 5 + 1 = 16 the remainder is added to the product to yield the dividend. |
 |
Partitive division
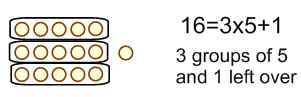
When direct modeling division, you must choose to either show a partitive picture or a measurement picture. A partitive picture for 16 ÷ 3 would have 16 divided into 3 groups:
Measurement division
A measurement division picture would have 16 divided into groups of 3:

In different problems, the remainder has different affects on the answer. Consider these examples:
Ex. 1: Five children will share 14 cookies. How many cookies will each child get? How many will be left over?
Notice that this problem asks specifically for the remainder as well as the product. When we work out this problem, we find that each child gets 2 cookies, and 4 cookies are left over.

What happens to the remainder is that it is left over, as the question suggests. Each child gets 2 cookies--the quotient.
Ex. 2: There are 12 cookies. I will give 5 cookies to each child. How many children get cookies?
This problem questiond doesn't specifically ask for the number left over, but it's clear when we work out the problem that 2 children get 5 cookies each and that the other 4 cookies are left overs.

Again, in this context, the remainder is just an amount left over, and the answer to the main question is the quotient: 2 children get cookies.
Ex 3: There are 14 children. A van can hold 5 children. How many vans are needed to take all of the children?
My picture is the same for this problem as for example 2, but I have to do something different with the remainder this time

Because the remainder can't be discarded this time, we add one more to the quotient: 3 vans are needed to take all of the children, which is one more than the quotient.
Ex. 4: 5 children will share 14 cookies (and they will cut left over cookies into pieces to share). How many cookies will each child get?
If you change the first example just a little--so that you're not assuming that the remainder is just an amount left over, theres another answer you can get.
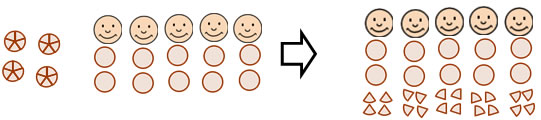
If we make the assumption that the cookies can be broken or cut into pieces, we can give the children partial cookies to use up the remainder, so that each child gets 2 4/5 cookies. The whole number 2 part of the answer is the whole number quotient. The fraction part of the answer has the remainder in the numerator and the divisor in the denominator.
![]()
This problem, FYI, is a little too hard for second or perhaps even third grade, but if we had 4 children sharing 15 cookies so that the cookies could be shared by making halves and quarters the problem would not be too hard for second grade. Children can solve problems with fractions in second grade if the fractions are friendly to think about, and the friendliest fractions are halves and quarters (beause a quarter is half of a half).
Ex 5: I made 14 cookies. If I make as many plates of 5 cookies each as I can for the bake sale, how many cookies will be left over for me?

This is kind of an unusual question, because it isn't asking for the groups at all--it's asking for the remainder.
The names of the parts of a division problem are dividend ÷ divisor = quotient R=remainder
Division problems can be figured out either by direct modeling using either a partition or a measurement division interpretation.
The natural way (splitting into groups) of solving a partition division problem works well only if you're dividing by 2 or 4.
The natural way (skip counting until you reach the dividend) of solving a measurement division problem works well for children who are good at skip counting.
Division problems can also be figured out by thinking about the missing number multiplication problem.
If the dividend isn't divided evenly (if there's a remainder), then when multiplying you need to ask yourself: what can I multiply the divisor by to get as close as possible to the dividend without going over that number.
The multiplication way of representing this relationship is divisor × quotient + remainder = dividend
When you have a division word problem that has a remainder, the sensible answer to the word problem question can be:
The right answer to the question depends on making sense of what the question is asking. Sometimes, either the "quotient" or the "quotient + a fraction" answer would make sense, and what you as a teacher might be looking for depends on what the class is studying.