Lesson 6.3: Area and Volume. More discussion of area, and volume concepts at the third grade level.

Recap of area:

Basic idea of area: The biggest and most important idea of area is that it is the number of square units that fill or cover a (2-dimensional) shape. This idea is more central than any of the formulas that let you find areas of shapes because it is the idea that all of the formulas come from. Children should have experiences with filling or covering irregular shapes with square units to find the area as well as experiences where they can multiply to find rectangular areas.

A common misconception is that area is defined as length times width and that the length times width formula can be used to find the area of all shapes.

Connections between area and learning multiplication: Finding the area of a rectangle by multiplying and showing multiplying by drawing a rectangle are closely related and reinforce each other.

Recall that drawing a rectangle or an array is an important way of representing multiplication. Further, you can connect this representation to the earlier repeated addition model for multiplication by adding up the rows or the columns:

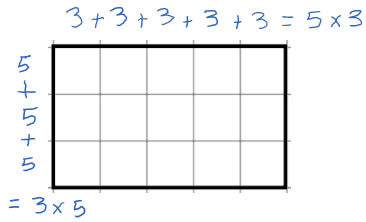This diagram shows that the area of the rectangle can be found by multiplying the side lengths (and that multiplying the side lengths is the same as using repeated addition to find the product). This diagram is also the main way of showing and explaining the commutative property. The commutative property says that you can multiply numbers in either order: 3 fives is the same as 5 threes.

The distributive law: We can also use the rectangle area representation for multiplication to show the distributive law of multiplication. This goal shows up twice in the standards: once in Operations and Algebraic thinking, and once in Measurement.

This diagram shows the distributive law as described in the measurement standard above:

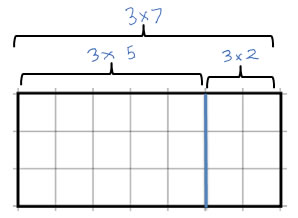This diagram that shows the distributive law for the example: 3 × (5 + 2) = (3 × 5) + (3 × 2) It uses part b of the 3rd grade measurement standard 7 by showing the multiplication problem as an area on a grid. It shows the distributive law relationship described in part c of the standard.: 3 × (5 + 2) = (3 × 5) + (3 × 2) It also uses the concept from part d of the standard, that area is additive: if you break a shape into two pieces and add their areas, that gives you the total area. CCSS.Math.Content.3.MD.C.7d Recognize area as additive. Find areas of rectilinear figures by decomposing them into non-overlapping rectangles and adding the areas of the non-overlapping parts, applying this technique to solve real world problems.

• Make sure you remember how to show the distributive law in this way.

More about area and perimeter: For the assignment for the last lesson on area and perimeter, you experimented with making rectangles all of which had the same area, but some of which had different perimeters. Let's look at the other version: what if you had different shapes, all with the same perimeter? When you investigates shapes with the same area, you built them out of the same number of square tiles: number of square tiles is a way of counting and figuring out area. To investigate shapes with the same perimeter, you could tie a piece, of string, or tape together a strip of paper to make something that will keep the same length (perimeter), but you can change the shape, which might change the area.

For example, all of these shapes have the same perimeter of 20 cm:

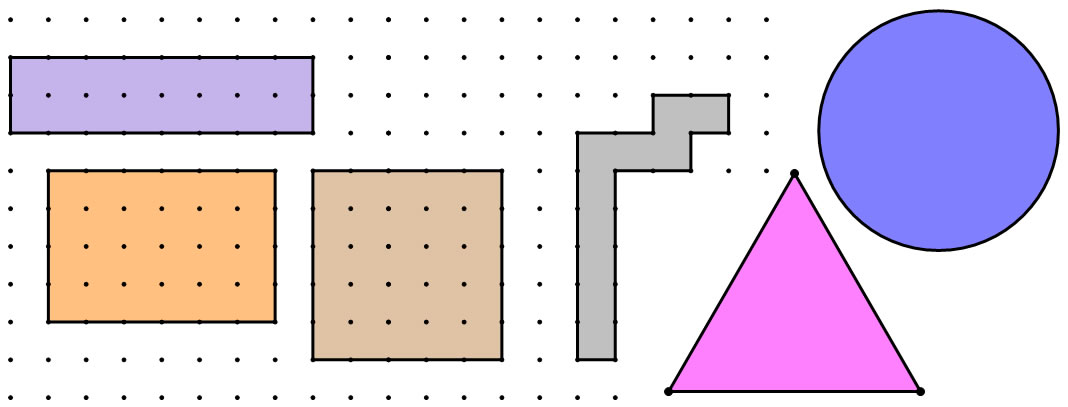
Which of the rectangles do you think has the largest area? Which of all the shapes do you think has the largest area?

Here's an experiment to try:

• Make a loop out of a strip of paper or a length of ribbon by taping the ends together.
• Now set it on the table top, and fill it with the unit cubes from your math kit.
• Fit in a long line of cubes from left to right making the line as long as you can.
• Now take the cubes and rearrange them in your paper strip: can you fit in any more cubes? Probably you can. If you keep stuffing in cubes, your paper strip gets fatter--more square/ocagonal/circular.
• If you poured beans or marbles or rice into your paper strip, it would push the strip in all directions until it's nearly circular (if you can keep the beans from escaping under the strip)

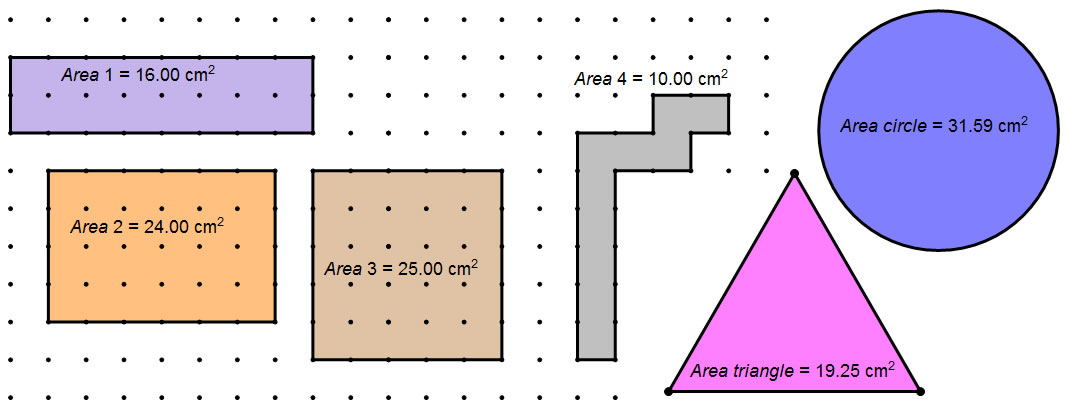
Here are the areas of of the shapes in the first picture. The area of the square is the largest of all of the rectangles, and the area of the circle is the largest of all of the shapes total. The squiggly shape that's only 1 cm wide has the smallest area.

If you look at all of the shapes with the same perimeter, the one with the largest area will be the one that is closest to being a circle.

A square (because it's length and width are equal) is the rectangle that is closest to being a circle. The square has the biggest area of all of the rectangles.

Volume in Third grade:

In fifth grade, children learn to measure and calculate volume in cubic units. In third grade, children learn to measure and estimate volume and weight in units that are intended for measuring liquids rather than geometric shapes.

Children should measure volumes of things that are pour-able (liquids, rice, flour, sugar) by using tools like measuring cups. The units we use to measure volumes in third grade are things like cups, gallons, liters and milliliters. They are the sorts of measurements you use when cooking or measuring a liquid. Children should use the sorts of measurement tools you use for cooking to measure volumes.

Despite not working with geometric formulas, there are important things to learn about estimation with volumes. Volume can be tricky: the same amount of water in a fat glass will look taller than you expect in a thin glass. If you make two play-dough balls: one using 1 cup of play-dough, and another using 1/2 cup of playdough, the smaller one will look like it is more than half the size of the larger one because while it's volume is half, it's height is more than half. Experience with measuring and working with different volumes can help children develop good estimation skills for volume.

The larger marble in the picture is about 1 1/2 times as wide as the smaller one, but it's about 4 times as heavy.

Children should also work with weight and mass using tools like scales. The same things that are tricky about volume are also tricky about weight (weight and volume are closely related for most objects), so experience really helps with estimation skills (estimating weight and volume requires a little different way of thinking from estimating length).

In fifth grade, children will be using geometric formulas to calculate volumes. When you use geometric formulas, you have different, but related, units of measurement. A common fifth-grade measurement unit is 1 cubic centimeter. The unit cubes with your base 10 blocks are 1 cubic centimeter. That's the same volume as 1 milliliter, but we use the units of milliliters in third grade, and cubic centimeters in fifth grade (mostly).