Children "analyze and compare two- and three-dimensional shapes" and describe similarities, differences and attributes (K.G.4). Attributes are the same things as properties--they are things that we describe as being the same or different between shapes. In first grade, children should "distinguish between defining attributes ... versus non-defining attributes... [and] build and draw shapes to possess defining attributes." (1.G.1) Lesson 1 discussed defining attributes of the standard shapes (triangle, square, rectangle), this lesson looks at geometric attributes that are shared by some triangles or quadrilaterals. This ties into "recogniz[ing] and draw[ing] shapes having specified attributes" (2.G.1) and "understand[ing] that shapes in different categories ... may share attributes... , and that the shared attributes can define a larger category" (3.G.1).
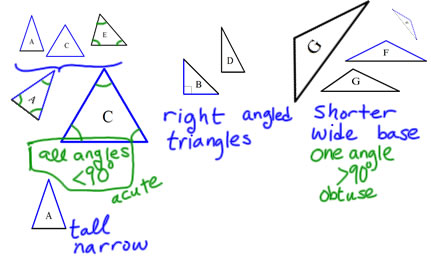
Sorting triangles by angle measurements

Angles are categorized as right (if their measurement is 90°--half of a straight angle), acute (if it is less than a right angle) or obtuse (if it is greater than a right angle. One way of translating that into classifying about triangles is to say that it is obtuse if its largest angle is obtuse, right if its largest angle is right, and acute if its largest angle is acute. Sometimes that seems a little confusing with, for example, an equilateral triangle where all of the angles are the same size, so another way to describe acute triangles is that they have all 3 angles acute.
These categories fit nicely--the triangles look like they go together. Children likely to first describe the triangles using informal language (tall and narrow/short and wide). The more formal language that we use to describe the triangles by their angles is important, however, for understanding shapes because it turns a description that makes most sense if the triangles are in one orientation (with a particular side horizontally on the bottom) to a description that makes sense for the triangles no matter how you turn them. You can, for instance, turn a tall narrow triangle into a short, wide triangle by turning it on its side, but when we come up with attributes to describe geometric shapes, we want to use attributes and descriptions that don't change when we turn the triangle.
Sorting triangles by side lengths
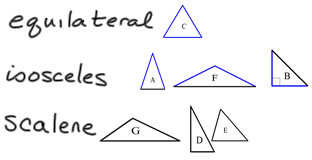
Triangles are called equilateral if all of the sides have the same length.
Triangles are called isosceles if two sides are the same length. Sometimes in math class we say that triangles are isosceles if they have two and only two sides the same length, and sometimes we say that they are isosceles if they have at least two triangles the same length. Probably it's safer to say that triangles are isosceles if they have at least two sides the same length--that means equilateral triangles are a special kind of isosceles triangle, just like squares are a special kind of rectangle.
Triangles are called scalene if all of the sides are different lengths.
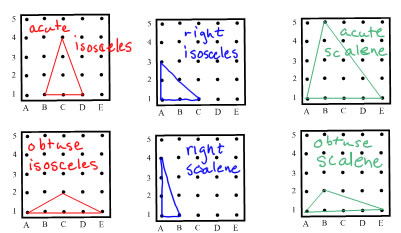
Each triangle can be sorted both by their side lengths and by their angle measures
Isosceles triangles can be acute, right or obtuse
Scalene triangles can be acute, right or obtuse
Equilateral triangles are always acute, they are never right or obtuse.
You can make all of the kinds of isosceles and scalene triangles on a geoboard, but you can never make an equilateral triangle on a geoboard (you can get really close, but not quite).
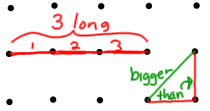
An extra note about geoboards:
When you're looking at measurements on a geoboard there are a couple of mistakes it's easy to make. The first is that when you are measuring lengths, you could be counting dots instead of lengths in between. The length should be the number of spaces (think of each space as an inch), not the number of dots. The other thing to watch out for is that you can't just count diagonally to find diagonal lengths. The distance between two diagonally adjacent pegs is greater than the vertical or horizontal distance between two adjacent pegs. (It's not a simple fraction to tell how much longer, either--you need the Pythagorean theorem for that!) |
 |
Quadrilaterals
Polygons that have 4 sides are quadrilaterals. There are even more named varieties of quadrilaterals than there are varieties of triangles. All of the shapes in this image are quadrilaterals
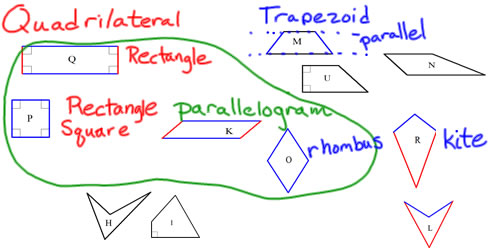
One property that quadrilaterals can have is that they can have parallel opposite sides. If each side has a parallel opposite side (two pairs of parallel sides), the shape can be called a parallelogram. Everything in the green loop is a parallelogram. Rectangles, squares and rhombuses (rhombi) are parallelograms because their opposite sides are always parallel. It's also correct to say that a quadrilateral is a parallelogram if its opposite sides are the same length, but usually in the definition we use that the opposite sides are parallel because the word parallel is part of parallelogram.
A rhombus has all 4 sides equal length. O is a rhombus, and it's sneaky, but the square P is a rhombus too. (Squares get to be a lot of different things besides just squares).
Quadrilaterals that have one pair of parallel sides are called trapezoids. M, N and U are all trapezoids. Some math books (and lots of mathematicians) say that a trapezoid has at least on pair of parallel sides, so that would make a parallelogram (with two pairs of parallel sides like K, O, P and Q) just a special kind of a trapezoid. Other math books (includingmost of the high school geometry books I've looked at recently) say that trapezoids have one and only one pair of parallel sides. Because words get their meaning from what groups of people agree that they mean, there isn't a right or a wrong definition of trapezoid.
Sometimes we give special names to other shapes too. R, for instance, is a kite because it has two pairs of sides that are adjacent (next to each other) that are the same length. Like "trapezoid", there isn't just one definition of "kite"--some people would say that L is also a kite because it has two pairs of adjacent sides that are the same length, and other people would say it is not a kite because it's concave.
Every triangle can be classified by its angles and by its side lengths, but there are some quadrilaterals that don't have any special classification at all. H and I, for example, aren't part of any named group of quadrilaterals.
One important idea about classifying shapes is that the same shape can fit into more than one category, and some categories are subsets of other categories. For example:
| A square is a special kind of rectangle. All squares are rectangles. Some rectangles are squares, and some rectangles are not squares. | 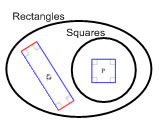 |
| A square is also a special kind of a rhombus. All squares are rhombi (or rhombuses). Some rhombi are squares, and some are not squares. | 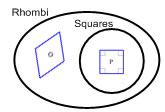 |
| A square is a rectangle and also a rhombus. Everything that is both a rectangle (90° angles) and a rhombus (all equal sides) is a square. | 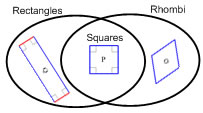 |
| Squares, rectangles and rhombi all have parallel sides, so they are all parallelograms. There are some parallelograms that don't fit rectangles, rhombi or squares. | 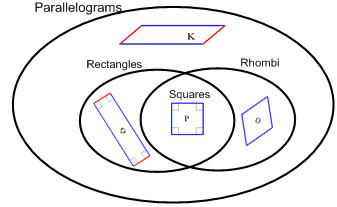 |
All of these shapes (as well as trapezoids, kites, and a few others) are quadrilaterals because they all have 4 sides.